Решение. Для каждого года квартальные уровни укрупним до годовых и по ним исчислим темпы роста

Для каждого года квартальные уровни укрупним до годовых и по ним исчислим темпы роста.

Таблица 8.7

Динамика поставки сельскохозяйственной

продукции торговой фирме

Годы	Годовые уровни, тыс. т	Темпы роста, %
к предыдущему году	к первому году
Первый	66,0	-	100,0
Второй	69,4	105,2	105,2
Третий	74,2	106,9	112,4

Можно отметить, что ряд динамики имеет четкую тенденцию роста поставок, об этом свидетельствуют увеличивающиеся цепные и базисные темпы роста.

Для расчета индексов сезонности в таких рядах динамики применяют формулу:

Определим теоретические значения по уравнению:

Для определения параметров а ₀ и а ₁ составим таблицу 8.8 со вспомогательными расчетами.

Таблица 8.8

Расчет параметров 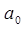и 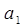аналитического уравнения

Периоды	Поставка, тыс.т,	t	t^2	yit
Первый год
I кв.	16,2	-11		-178,2	16,2	100,0
II кв.	17,0	-9		-153,0	16,4	103,7
III кв.	17,7	-7		-123,9	16,7	106,0
IV кв.	15,1	-5		-75,5	16,9	89,3
Второй год
I кв.	15,2	-3		-45,6	17,1	88,9
II кв.	19,4	-1		-19,4	17,4	111,5
III кв.	18,0			18,8	17,6	102,3
IV кв.	16,8			50,4	17,9	93,9
Третий год
I кв.	15,8			79,0	18,1	87,3
II кв.	22,5			157,5	18,3	117,5
III кв.	18,7			168,3	18,6	100,5
IV кв.	17,2			189,2	18,8	91,5
Итого	209,6			66,8	210,0	-

Определим параметры: ;

Следовательно, уравнение прямой примет вид: . Подставив в полученное уравнение значения t (квартальные), получим выравненные уровни ряда (табл. 8.8 гр. 6). Далее необходимо оп-ределить для каждого квартала процентные отношения эмпирических уровней ряда (y_i) к теоретическим (), т.е. (табл.8.8 гр.7).

Таблица 8.9

Динамика поставок сельскохозяйственной продукции торговой фирме и расчет индексов сезонности

Квар- талы	Фактические данные, yi	Выравненные данные,	Фактические данные в % к выравненным,	Сумма про-центных отноше ний, (гр.8+ +гр.9+ +гр.10)	Индексы сезон- ности, : : n
первый год	второй год	третий год	первый год	второй год	третий год	первый год	второй год	третий год
1	2	3	4	5	6	7	8	9	10	11	12
I	16,2	15,2	15,8	16,5	17,1	18,1	100,0	88,9	87,3	276,2	92,1
II	17,0	19,4	22,5	16,4	17,4	18,3	103,7	111,5	117,5	332,7	110,9
III	17,7	18,0	18,7	16,7	17,6	18,6	106,0	102,3	100,5	308,8	102,9
IV	15,1	16,8	17,2	16,9	17,9	18,8	89,3	93,9	91,5	274,7	91,6
Итого	66,0	69,4	74,2	66,2	70,0	73,8	-	-	-	-

Просуммируем полученные процентные отношения за три года по одноименным кварталам:

I кв.: 100,00 + 88,9 + 87,3 = 276,2;

II кв.: 100,3 + 111,5 + 117,5 = 332,3 и т. д. (табл. 8.9 гр.11).

Затем исчислим индексы сезонности (табл. 8.9 гр.12). Они характеризуют размеры поставок сельскохозяйственной продукции в зависимости от времени года. Наибольший удельный вес поставок приходится на второй и третий кварталы года.

Пример 4. На условных данных о грузообороте предприятий в одном из регионов необходимо произвести выравнивание по ряду Фурье. В таблице содержатся произведения у · соs t, у · sin t, необходи-мые для определения параметров уравнения по первой гармонике.

На основе полученных итоговых данных таблицы 8.10 находим:

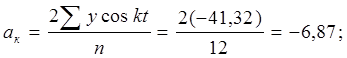
Отсюда:

Подставляя в это уравнение значения соs t, sin t (из таблицы приложения 2) получим теоретические значения грузооборота 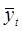(см. гр. 5 табл. 8.10).

Таблица 8.10

Грузооборот транспортных предприятий региона и расчет параметров системы уравнения по ряду Фурье

Месяц, t	Грузооборот, млрд. ткм, у	у соs t	у sin t
1	2	3	4	5
		60,00		71,20
		69,28	40,00	81,02
		43,00	74,45	90,22
			108,00	96,03
		- 67,00	116,04	97,10
		- 50,22	29,00	93,06
		- 70,00		85,04
		- 58,88	- 34,00	76,50
		-45,00	- 77,94	66,10
			- 70,00	60,26
		29,00	- 50,22	59,22
		48,50	- 28,00	63,26
Итого		- 41,32	107,36	939,04

Параметры гармоники второго и высшего порядка рассчитываются аналогично, и их значения последовательно присоединяются к значениям первой гармоники. Опустив расчеты, запишем уравнение для выравнивания изучаемого ряда с учетом второй гармоники:

Подставив в данное уравнение конкретные значения соs t,sin t, sin 2t, соs 2t, получим выравненные данные грузооборота по месяцам. Расчет и сравнение остаточных дисперсий позволяет судить о том, какая гармоника наиболее близка к фактическим уровням ряда.

Дата добавления: 2014-11-25