
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Шкала Чеддока
|
|
|
|
| Величина показателя тесноты связи по абсолютной величине | 0,1 - 0,3 | 0,3 - 0,5 | 0,5 - 0,7 | 0,7 - 0,9 | 0,9 - 0,99 |
| Характеристика связи | Сла бая | Умерен ная | Замет ная | Высокая (тесная) | Весьма высокая (очень тесная) |
Корреляционно-регрессионный анализ. Корреляционной связью между двумя признаками называется такая связь, при которой изменение среднего значения факторного признака вызывает изменение среднего значения результативного.
Конечная цель статистического изучения корреляционной связи состоит в получении статистической модели этой зависимости в форме уравнения регрессии или уравнения связи. Решение этой задачи осуществляется в следующей последовательности.
1.Осуществляется логический анализ сущности изучаемого явления и причинно-следственных связей, т.е. устанавливается результативный признак ( ) и фактор (или факторы) его изменения (х1,х2,…
) и фактор (или факторы) его изменения (х1,х2,…  ). Связь двух признаков является парной корреляцией, а нескольких - множественной.
). Связь двух признаков является парной корреляцией, а нескольких - множественной.
2. Проверка требований, предъявляемых к факторным и результативным признакам:
- однородность распределения, т.е. коэффициенты вариации не должны превышать 33 %: Vу ≤  ,
, 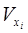 ≤
≤ 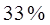 ;
;
- соответствие нормальному закону распределения, - чаще всего используется правило “трех сигм”.
Если  и
и  , то с вероятностью 0,997 можно утверждать, что распределение соответствующих признаков (ре-зультативного и факторного) соответствуют нормальному закону распределения.
, то с вероятностью 0,997 можно утверждать, что распределение соответствующих признаков (ре-зультативного и факторного) соответствуют нормальному закону распределения.
- независимость по объектам наблюдения. Если рассматривается статическое распределение или ряды распределения, то это требование подтверждается путем логического анализа, т.е. apriori. В то же время при построении регрессионных моделей по рядам динамики дополнительно необходимо проверять гипотезы об отсутствии автокорреляции и тенденции в рядах динами (стр.325-326. данного раздела);
- отсутствие мультиколлинеарности между факторными признаками (при множественной корреляции), т.е.  и
и  (
(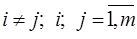 ) не должны быть связаны между собой ни функциональной (мультипликативной или аддитивной), ни тесной корреляционной связью, т.е.
) не должны быть связаны между собой ни функциональной (мультипликативной или аддитивной), ни тесной корреляционной связью, т.е.  или
или  , k є
, k є 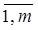 ; или
; или  ≤ 0,8.
≤ 0,8.
- все факторные и результативные признаки должны иметь количественное выражение и взаимно соответствовать друг другу в пространстве, т.е. по объектам наблюдения, и по времени.
3. Исключение из массива первичной информации всех резко-выделяющихся (аномальных) единиц признаков-факторов и форми-рование нового массива для последующего анализа.
4. Определение формы и направления связи. В случае парных зависимостей применяются: содержательный анализ, графический метод, метод аналитических группировок и построение корреляцион-ных таблиц.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 1452; Нарушение авторских прав?; Мы поможем в написании вашей работы!