Гармонический осциллятор и осциллятор с затуханием. Параметры моделей. Связь между кинематическими характеристиками

Гармонический осциллятор - колеблющаяся система, потенциальная энергия которой пропорциональна квадрату отклонения от положения равновесия.

Колебательная система - совокупность тел, способных совершать движения, многократно повторяющиеся или приблизительно повторяющиеся через определенные промежутки времени.

23.Описание состояния абсолютно твердого тела. Разложение движения твердого тела на поступательное и вращательное. Углы Эйлера.

Углы Эйлера — углы, описывающие поворот абсолютно твердого тела в трёхмерном евклидовом пространстве. В математике термин евкли́дово простра́нство может обозначать один из сходных и тесно связанных объектов: В обоих случаях, n-мерное евклидово пространство обычно обозначается , хотя часто используется не вполне приемлемое обозначение .1. Конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму: 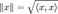, в простейшем случае (евклидова норма): , где 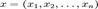(в евклидо вом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант). Иначе говоря евклидово пространство — конечномерное гильбертово пространство. 2. Метрическое пространство, которое является конечномерным векторным пространством над полем вещественных чисел с евклидовой метрикой, введённой по формуле:

, где и , то есть с функцией расстояния, порождаемой описанной выше нормой. Замечание: часто под евклидовой метрикой понимают метрический тензор, порождающий соответствующее скалярное произведение, норму и функцию расстояния, то есть постоянный (матрица которого не зависит от координат, при должном их выборе) положительно определенный (риманов) метрический тензор, делающий многообразие (или его конечную область) евклидовым пространством (или конечной областью евклидова пространства). Таким образом, евклидова метрика в этом смысле означает положительно определенный метрический тензор без кривизны, причем часто имеется в виду еще и выбор координат, делающий представление метрического тензора единичной матрицей δ _ij. Иногда под локальной евклидовостью понимают также то, что риманова метрика (выбором координат) может быть приведена к евклидовскому виду в бесконечно малой окрестности выбранной точки многообразия.

Дата добавления: 2014-11-25