Стационарное течение идеальной жидкости

Эффект Доплера.

ДОПЛЕРА ЭФФЕКТ, изменение воспринимаемой частоты колебаний, обусловленное движением источника или приемника волн, либо и того и другого; впервые теоретически обоснован в 1842 К.Доплером (1803-1853). Данный эффект особенно заметен в случае звуковых волн, примером чему может служить изменение воспринимаемой высоты тона гудка проходящего мимо поезда. Возникновение эффекта поясняется рисунком, на котором источник волн движется влево со скоростью v относительно неподвижного наблюдателя ("приемника"). За время t = t ₁  t ₀ источник проходит расстояние vt. Если l — длина волны испускаемого звука, то число волн, укладывающихся в промежутке между источником и приемником, увеличивается на vt / l. Если частота звука f_e, то за время t испускается f_et волн. Но число f_rt волн, достигших приемника, меньше, чем испущено источником, на величину vt / l. Отсюда следует, что .

Уравнение Эйлера — одно из основных уравнений гидродинамики идеальной жидкости. Названо в честь Л.Эйлера, получившего это уравнение в 1755 году. По своей сути является уравнением движения жидкости.

Рассмотрим движение идеальной жидкости. Выделим внутри неё некоторый объём V. Согласно второму закону Ньютона, ускорение центра масс этого объёма пропорционально полной силе, действующей на него. В случае идеальной жидкости эта сила сводится к давлению окружающей объём жидкости и, возможно, воздействию внешних силовых полей. Предположим, что это поле представляет собой силы инерции или гравитации, так что эта сила пропорциональна напряжённости поля и массе элемента объёма. Тогда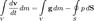

где S — поверхность выделенного объёма, g — напряжённость поля. Переходя, согласно формуле Гаусса — Остроградского, от поверхностного интеграла к объёмному и учитывая, что , где ρ — плотность жидкости в данной точке, получим: 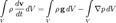В силу произвольности объёма V подынтегральные функции должны быть равны в любой точке: Выражая конвективную производную через частные производные: получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести: ,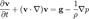

где — плотность жидкости, — давление в жидкости, — вектор скорости жидкости, — вектор напряжённости силового поля, — оператор набла для трёхмерного декартового пространства.

Дата добавления: 2014-11-25