Давление жидкости и газа в поле силы тяжести. Барометрическая формула. Жидкостный манометр

Классификация деформаций. Упругий

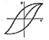Гистерезис (от греч. hysteresis — отставание, запаздывание), явление, которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность), неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля). Г. наблюдается в тех случаях, когда состояние тела в данный момент времени определяется внешними условиями не только в тот же, но и в предшествующие моменты времени. Неоднозначная зависимость величин наблюдается в любых процессах, т.к. для изменения состояния тела всегда требуется определённое время (время релаксации) и реакция тела отстаёт от вызывающих её причин. Такое отставание тем меньше, чем медленнее изменяются внешние условия Однако для некоторых процессов отставание при замедлении изменения внешних условий не уменьшается. В этих случаях неоднозначную зависимость величин называется гистерезисной, а само явление — Г.

Упругий Г., т. е. гистерезисная зависимость деформации и от механического напряжения s, наблюдается в любых реальных материалах при достаточно больших напряжениях (рис. 6). Упругий Г. возникает всякий раз, когда имеет место пластическая (неупругая) деформация (см. Пластичность). Пластическая деформация обусловлена перемещением дефектов, например дислокаций, всегда присутствующих в реальных материалах. Примеси, включения и др. дефекты, а также сама кристаллическая решётка стремятся удержать дислокацию в определенных положениях в кристалле. Поэтому требуются напряжения достаточной величины, чтобы сдвинуть дислокацию. Механическая обработка и введение примесей приводят к закреплению дислокаций, в результате чего происходит упрочнение материала, пластическая деформация и упругий Г. наблюдаются при больших напряжениях. Энергия, теряемая в образце за один цикл, идёт в конечном счёте на нагревание образца. Потери на упругий Г. дают вклад во внутреннее трение. В случае упругих деформаций, помимо гистерезисных, есть и др. потери, например обусловленные вязкостью. Величина этих потерь, в отличие от гистерезисных, зависит от частоты изменения s (или и). Иногда понятие «упругий Г.» употребляется шире — говорят о динамической петле упругого Г., включающей все потери на данной частоте.

Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности. Для тонкого растяжимого стержня закон Гука имеет вид: . Здесь сила натяжения стержня, — его удлинение, а называется коэффициентом упругости (или жёсткостью). Очевидно, что коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Полезно выделить зависимость от размеров стержня (площади поперечного сечения и длины ) явно, записав коэффициент упругости как . Величина называется модулем Юнга и зависит только от свойств материала. Полезно теперь ввести относительное удлинение и нормальное напряжение в поперечном сечении . В этих обозначениях закон Гука записывается как . Величину, обратную жёсткости, называют гибкостью.

Обобщённый закон Гука

В общем случае напряжения и деформации являются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонентов). Связывающий их тензор упругих постоянных является тензором четвёртого ранга и содержит 81 коэффициент. Вследствие симметрии тензора , а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом: 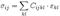. Для изотропного материала тензор содержит только два независимых коэффициента. Следует иметь ввиду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Манометр (от греч. manуs — редкий, неплотный и...метр), прибор для измерений давления жидкостей и газов. Различают М. для измерений абсолютного давления, отсчитываемого от нуля (полного вакуума); М. для измерений избыточного давления, то есть разности между абсолютным и атмосферным давлением, когда абсолютное давление больше атмосферного; дифманометры для измерений разности двух давлений, каждое из которых, как правило, отличается от атмосферного. Для измерений давления, соответствующего атмосферному, применяют барометры, для измерений давления разреженных газов — вакуумметры (главным образом в вакуумной технике). Основа измерительной системы М. — чувствительный элемент, являющийся первичным преобразователем давления. В зависимости от принципа действия и конструкции чувствительного элемента различают М. жидкостные, поршневые, деформационные (пружинные). Кроме того, находят применение приборы, действие которых основано на измерении изменений физических свойств различных веществ под действием давления. В жидкостных М. чувствительным элементом является столб жидкости, уравновешивающий измеряемое давление. Идея использовать жидкость для измерения давления принадлежит итальянскому учёному Э. Торричелли (1640). Первые ртутные М. были сделаны итальянским механиком В. Вивиани (1642) и французским учёным Б. Паскалем (1646). Конструктивное исполнение жидкостных М. отличается большим разнообразием. Основные разновидности жидкостных М.: U-oбразные (двухтрубные), чашечные (однотрубные) и двухчашечные. Современные жидкостные М. имеют пределы измерений от 0,1 н/м² до 0,25 Мн/м² (~ от 0,01 мм вод. cm. до 1900 мм pm. cm.) и находят применение главным образом для измерений с высокой точностью в лабораторных условиях. Жидкостные М., служащие для измерения малых избыточных давлений и разрежений менее 5 кн/м² (37,5 мм pm. ст.), называются микроманометрами. При малых пределах измерений жидкостные М. заполняются лёгкими жидкостями (вода, спирт, толуол, силиконовые масла), а при увеличении пределов измерений — ртутью. При измерении давления чашечным микроманометром (рис. 2) заполняющая сосуд жидкость вытесняется в трубку, изменение уровня жидкости сравнивают со шкалой, отградуированной в единицах давления. Пределы измерений прибора не превышают 2 кн/м² (~200 мм вод. ст.) при наибольшем угле наклона. Для точных измерений и поверки микроманометров др. типов применяют двухчашечные микроманометры компенсационного типа, в которых один из сосудов (чашка) жестко закреплен, а второй сосуд с целью создания необходимого для уравновешивания давления столба жидкости перемещается в вертикальном направлении. Перемещение, определяемое при помощи точной шкалы с нониусом или по концевым мерам длины, непосредственно характеризует измеряемое давление. Компенсационными микроманометрами можно измерять давления до 5 кн/м² (~500 мм вод. ст.), при этом погрешность не превышает (2—5)Ч10^-3 н/м², или (2—5)Ч10^{-2 мм вод. cm.} Верхний предел измерения жидкостных М. можно повысить, увеличив высоту столба жидкости и выбрав жидкость с большей плотностью. Однако даже при заполнении М. ртутью его верхний предел измерения редко превышает 0,25 Мн/м² (~1900 мм рт. ст.), например в чашечных М., в которых широкий сосуд сообщен с вертикальной трубкой. Жидкостные М. для измерений с высокой точностью оснащают электрическими или оптическими отсчётными устройствами, а их конструктивное исполнение позволяет устранить различные источники погрешностей (влияние температуры, воздействие вибраций, капиллярные силы и т. д.). Высокую точность обеспечивает двухчашечный ртутный М. абсолютного давления с так называемым ёмкостным отсчётом (рис. 3), который применяется для определения температуры в эталонном газовом термометре (Всесоюзный научно-исследовательский институт метрологии имени Д. И. Менделеева). Пределы измерений М. составляют (0—0,13) Мн/м² (0—1000 мм pm. ст.). Для улучшения эксплуатационных характеристик (в основном точности показаний) в жидкостных М. применяют следящие системы, которые позволяют автоматически определять высоту столба жидкости. В поршневых М. чувствительным элементом является поршень или другое тело, с помощью которого давление уравновешивается грузом или каким-либо силоизмерительным устройством. Распространение получил М. с так называемым неуплотнённым поршнем, в котором поршень притёрт к цилиндру с небольшим зазором и перемещается в нём в осевом направлении. Впервые подобный прибор был создан в 1833 русскими учёными Е. И. Парротом и Э. Х. Ленцем; широкое применение поршневые М. нашли во второй половине 19 века благодаря работам Е. Рухгольца (Германия) и А. Амага (Франция), которые независимо друг от друга предложили "неуплотнённый" поршень. Основное преимущество поршневых М. перед жидкостными заключается в возможности измерения ими больших давлений при сохранении высокой точности. Поршневой М. с относительно небольшими габаритами (высота ~0,5 м) превосходит по пределам измерений и точности 300-метровый ртутный М., конструкция которого была разработана французским учёным Л. Кальете (1891). М. был смонтирован на Эйфелевой башне в Париже. Верхний предел измерения поршневых М. составляет около 3,5 Гн/м² (3,5Ч10⁸ мм вод. ст.). При этом высота измерительной установки не превышает 2,5 м. Для измерения такого давления ртутным М. потребовалось бы довести его высоту до 26,5 км. Наиболее распространены грузопоршневые М. с простым неуплотнённым поршнем. Пространство под поршнем заполнено маслом, которое под давлением поступает в зазор между поршнем и цилиндром, что обеспечивает смазку трущихся поверхностей. Вращение поршня относительно цилиндра предотвращает появление контактного трения. Давление определяется весом грузов, уравновешивающих его, и площадью сечения поршня. Изменяя вес грузов и площадь сечения поршня, можно в широком диапазоне менять пределы измерений, которые для М. данного типа составляют 0,04—10 Мн/м² (0,4—100 кгс/см²). При этом погрешности наиболее точных эталонных М. не более 0,002—0,005 %. При дальнейшем повышении пределов измерений площадь поршня становится столь малой, что для грузов необходимо конструировать спец. устройства (опорные штанги, рычажные устройства). Например, для уменьшения веса грузов в М. системы М. К. Жоховского (СССР) уравновешивающее усилие создаётся при помощи гидравлического мультипликатора. В этом случае даже при измерении высоких давлений 2,5 Гн/м² (2,5Ч10⁴ кгс/см²) измерительная установка предельно компактна и не требует наложения большого числа грузов. Поршневые М. спец. конструкций применяются также при измерении небольших избыточных давлений, разрежений, абсолютного и атмосферного давлений. Как правило, поршневые системы таких М. предварительно уравновешиваются специальным устройством, что позволяет понизить нижний предел измерений практически до нуля. Поршень может быть уравновешен, например, пружинным механизмом. Вращение поршня осуществляется от электродвигателя. При создании разрежения в пространстве над верхней частью поршня избыток атмосферного давления уравновешивают грузы, накладываемые на его нижнюю часть.

Дата добавления: 2014-11-25