Цилиндрические поверхности 2 страница

b) точка пересечения вспомогательных прямых является центром дуги сопряжения;

c) 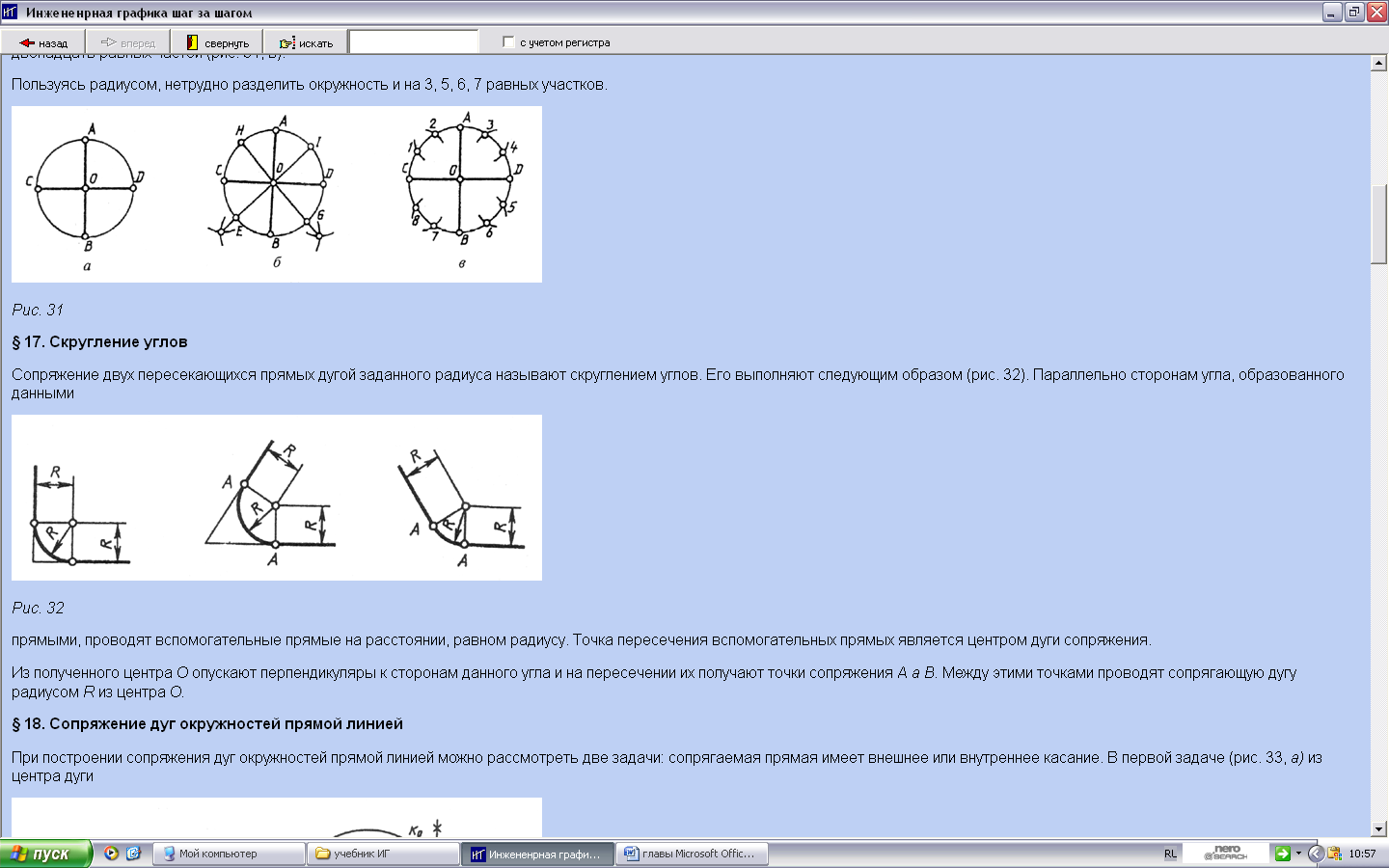из полученного центра О опускают перпендикуляры к сторонам данного угла;

d) на пересечении их получают точки сопряжения А (чаще в учебниках встречается обозначения точек сопряжения – К);

e) между этими точками проводят сопрягающую дугу радиусом R из центра О.

2. Сопряжение дуг окружностей прямой линией (касательные)

Построение прямых, касательных к окружностям, зависит от условия задачи. Может быть задана окружность с точкой касания, или окружность и точка, из которой следует провести касательную прямую, или две окружности, к которым нужно провести касательную прямую. Подход к решению этих задач будет различным, но во всех случаях существует одно правило: точка касания должна лежать на перпендикуляре, проведенном из центра окружности к прямой.

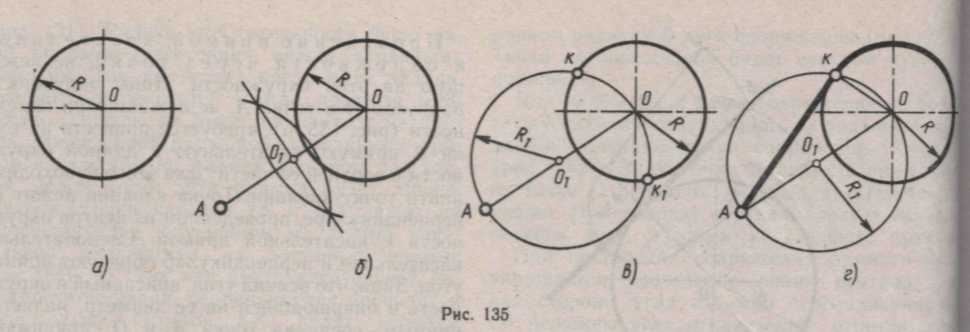
Проведение прямой, касательной к окружности через точку, лежащую на окружности, показано на рисунке справа (стр. 49). Так как точка касания лежит на перпендикуляре, проведенном из центра окружности к прямой, то касательную прямую следует проводить через заданную точку А перпендикулярно радиусу, соединяющему точку А с центром окружности О.

Проведение прямой, касательной к окружности через точку, не лежащую на этой окружности. Даны окружность радиусом R и точка А, не лежащая на окружности, требуется провести из точки А прямую, касательную к данной окружности в верхней ее части. Для этого необходимо найти точку касания. Точка касания лежит на перпендикуляре, проведенном из центра окружности к касательной прямой. Следовательно, касательная и перпендикуляр образуют прямой угол. Зная, что всякий угол, вписанный в окружность и опирающийся на ее диаметр, является прямым, соединив точки А и О, принимают отрезок АО за диаметр описанной окружности. В пересечении описанной окружности и окружности радиуса R будет находиться вершина прямого угла (точка К). Отрезок АО делят пополам, получают точку О₁ . Из центра О₁ радиусом, равным отрезку АО₁, проводят окружность, получают точки К и К₁ в пересечении с окружностью радиуса R. Так как нужно провести только одну касательную к верхней части окружности, выбирают нужную точку касания. Этой точкой будет точка К. Точку К соединяют с точками А и О, получают прямой угол, который опирается на диаметр АО описанной окружности радиусом R₁. Точка К — вершина этого угла, отрезки ОК и АК — стороны прямого угла, следовательно, точка К будет искомой точкой касания, а прямая АК — искомой касательной.

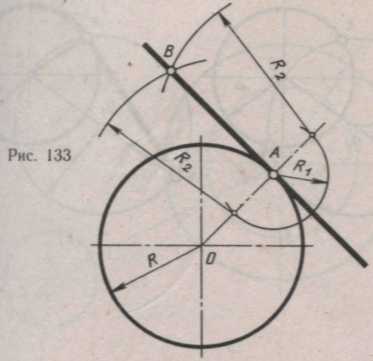
Проведение прямой, касательной к двум окружностям. Даны две окружности радиусами R и R₁, требуется построить касательную к ним. Возможны два случая касания: внешнее и внутреннее.

При внешнем касании касательная прямая находится с одной стороны от окружностей и не пересекает отрезок, соединяющий центры данных окружностей. При внутреннем касании касательная прямая находится с разных сторон от окружностей и пересекает отрезок, соединяющий центры окружностей.

Внешнее касание. Прежде всего необходимо найти точки касания. Известно, что они должны лежать на перпендикулярах, проведенных из центров окружностей (О и О₁) к касательной. Рассмотрим рис. г, где задача уже решена. Найденные точки касания К₁ и К₂ лежат на перпендикулярах О₁К₁ и ОК₂ . Если перемещать касательную К₁К₂ параллельно самой себе в направлении центров заданных окружностей, то точки К₁ и К₂ будут скользить по перпендикулярам О₁К₁ и ОК_2. В конце концов точка К₂ совпадет с центром О (окружности меньшего радиуса, а точка К₁ — с точкой К). Так как касательная K₁K₂ перемещалась параллельно самой себе, то отрезки К₂О и К₁К равны, и отрезок К₂О равен радиусу R. Через точку К из центра О₁ проводим вспомо­гательную окружность радиусом R₃= R₁ — R. Далее построение будет как в предыдущей задаче — проведение прямой, касательной к окружности, из заданной точки, не лежащей на этой окружности.

На рисунке, приведенном в пример ранее, показано поэтапное построение касательной к двум окружностям. Сначала строят касательную ОК из центра О к окружности радиуса R₂ (рис. а, б, в). Касательную ОК перемещают параллельно самой себе. Точки касательной при этом будут перемещаться по перпендикулярам к ней. Перпендикуляр О₁К, по которому перемещается точка К, продолжают до пересечения с заданной окружностью радиуса R₁, получают точку К₁. Из точки О перпендикулярно ОК или параллельно О₁К₁ проводят прямую. Она будет тем перпендикуляром, по которому перемещается второй конец касательной ОК. В пересечении этого перпендикуляра с окружностью радиуса R получают вторую точку касания — К_2. Соединив точки К₁ и К₂, получают внешнюю касательную к двум заданным окружностям (рис. г).

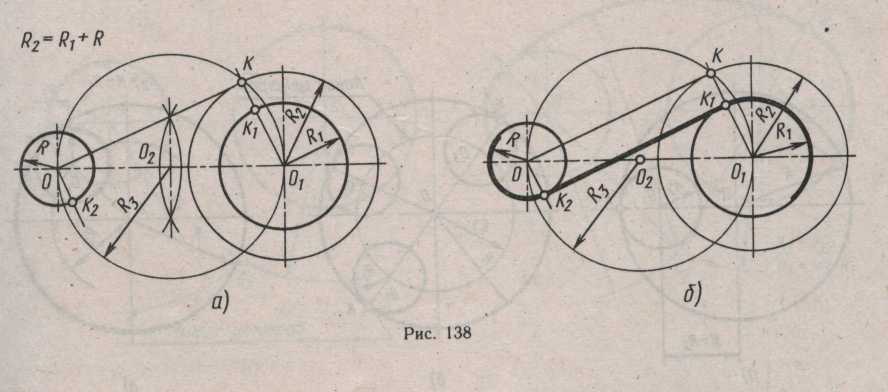
Внутреннее касание. Построение внутренней касательной к двум заданным окружностям выполняют аналогично построению внешней касательной, только вспомогательную окружной радиуса R₂ проводят из центра О₁ сумма радиусов R₂ =R₁+ R (рис. Выше на стр.50). Центры 0 и О₁ соединяют прямой и отрезок OO₁ делим пополам в точке О₂, из точки О₂ проводя окружность радиуса R₃, получают точку К. Точку К соединяют с центрами О и О₁. Отрезок О₁К пересекает окружность радиусом R₁ в точке К₁. Из центра О параллельно КО₁ проводят прямую до пересечения ее окружностью радиуса R в точке К₂. Точки К₂ и К₁ будут точками касания, соединив которые получают внутреннюю касательную двум заданным окружностям (рис. б).

3. Сопряжение двух дуг окружностей третьей дугой.

При построении сопряжения двух дуг окружностей третьей дугой заданного радиуса можно рассмотреть три случая:

ü когда сопрягающая дуга радиуса R касается заданных дуг радиусов R ₁ и R ₂ с внешней стороны;

ü когда она создает внутреннее касание;

ü когда сочетаются внутреннее и внешнее касания.

Построение центра О сопрягающей дуги радиуса R при внешнем касании осуществляется в следующем порядке: из центра О 1 радиусом, равным R + R 1, проводят вспомогательную дугу, а из центра O 2проводят вспомогательную дугу радиусом R + R 2. На пересечении дуг получают центр О сопрягаемой дуги радиуса R, а на пересечении радиусом R + R 1 и R + R 2 с дугами окружностей получают точки сопряжения А и А 1.
Построение центра О при внутреннем касании отличается тем, что из центра О 1 проводят вспомогательную окружность радиусом, равным R — R 1 а из центра О 2 радиусом R — R 2.
При сочетании внутреннего и внешнего касания из центра О 1 проводят вспомогательную окружность радиусом, равным R — R 1, а из центра О 2 — радиусом, равным R + R 2.

4. Сопряжение дуги окружности и прямой линии второй дугой

Здесь может быть рассмотрено два случая:

ü внешнее сопряжение и

ü внутреннее.

В том и в другом случае при построении сопрягающей дуги радиуса R центр сопряжения О лежит на пересечении геометрических мест точек, равно удаленных от прямой и дуги радиуса R на величину R ₁.

При построении внешнего сопряжения параллельно заданной прямой на расстоянии R 1 в сторону окружности проводят вспомогательную прямую, а из центра О радиусом, равным R + R 1,— вспомогательную окружность, и на их пересечении получают точку О 1 — центр сопрягающей окружности. Из этого центра радиусом R проводят сопрягающую дугу между точками А и А1, построение которых видно из чертежа.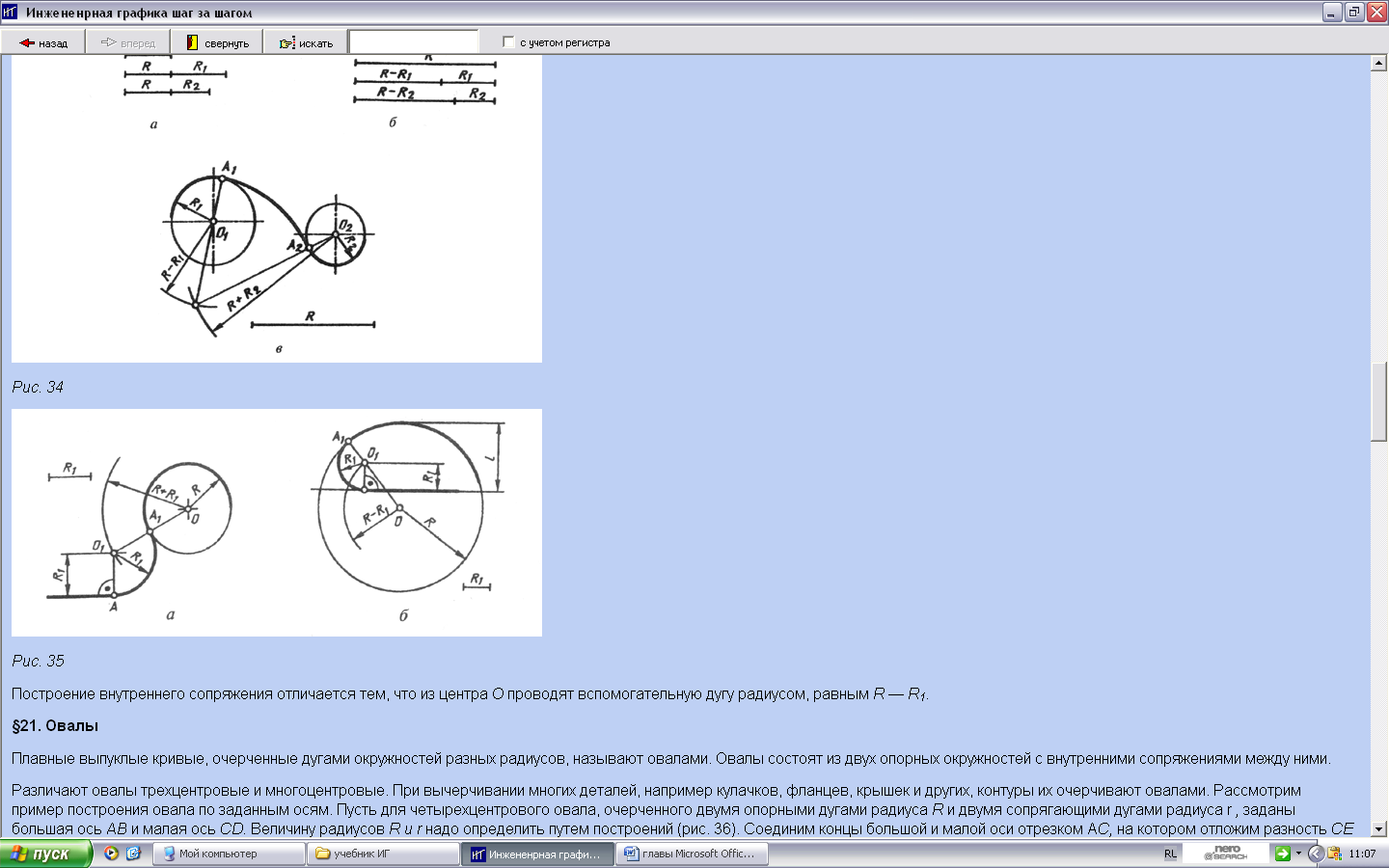
Построение внутреннего сопряжения отличается тем, что из центра О проводят вспомогательную дугу радиусом, равным R — R 1.

5. Овалы

Плавные выпуклые кривые, очерченные дугами окружностей разных радиусов, называют овалами. Овалы состоят из двух опорных окружностей с внутренними сопряжениями между ними.

Различают овалы трехцентровые и многоцентровые. При вычерчивании многих деталей, например кулачков, фланцев, крышек и других, контуры их очерчивают овалами. Рассмотрим пример построения овала по заданным осям. Пусть для четырехцентрового овала, очерченного двумя опорными дугами радиуса R и двумя сопрягающими дугами радиуса r, заданы большая ось АВ и малая ось CD. Величину радиусов R и r надо определить путем построений. Соединим концы большой и малой оси отрезком AС, на котором отложим разность СЕ большой и малой полуосей овала. Проведем перпендикуляр к середине отрезка AF, который пересечет большую и малую оси овала в точках О₁ и О₂. Эти точки будут центрами сопрягающихся дуг овала, а точка сопряжения будет лежать на самом перпендикуляре.

6. Лекальные кривые

Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс параболу, гиперболу, циклоиду, синусоиду эвольвенту и др.

7. Уклон и конусность.

Уклон. Поверхности деталей часто представляют собой плоскости, расположенные наклонно друг к другу. Например, в литых и штампованных деталях, в изделиях проката (рельсы, балки, швеллеры). На чертежах подобные плоскости изображаются прямыми линиями. При вычерчивании некоторых деталей угол наклона одной ее поверхности к другой выражают величиной уклона.

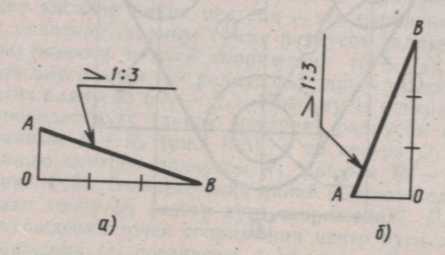Уклон прямой — это отношение противоположного катета АВ к прилежащему АС, т.е. tg α= 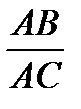. Уклоны выражают простой правильной дробью или в процентах.. Обозначается уклон знаком, размеры которого показаны на рисунке, согласно ГОСТ 2.304—81. Знак ставится перед числовым значением уклона над полкой линии выноски. Линия выноски заканчивается стрелкой, упирающейся в линию уклона. Острый угол знака должен быть направлен в ту же сторону, что и острый угол уклона.

Рассмотрим построение уклона, заданного отношением 1:3, относительно вертикального и горизонтального направлений. Сначала строят прямой угол АОВ. При горизонтальном направлении уклонаоткладывают отрезок произвольной величины по вертикальной стороне угла, получают точку А, а при вертикальном направлении уклона— по горизонтальной стороне угла. По второй стороне угла откладывают три таких отрезка, получают точку В. Соединив точки А и В прямыми, получают прямо­угольный треугольник, гипотенуза которого будет располагаться под заданным уклоном.

На рисунке (см. выше) уклон задан в процентах (15%). В этом случае строят прямой угол с вершиной О. На одной стороне угла (в данном случае горизонтальной) от точки О откладывают величину, принятую за 100%, например 100 мм, а на второй — от той же точки О откладывают величину, равную процентам заданного уклона, в данном случае 15 мм. Полученные точки соединяют прямой, которая будет располагаться с заданным уклоном.

Провести прямую с заданным уклоном через заданную точку можно, построив на свободном месте чертежа заданный уклон, потом с по­мощью двух угольников, параллельно по­строенному уклону, провести через заданную точку прямую.

Конусность — это отношение диаметра окружности основания прямого конуса к его высоте 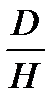, а для усеченного конуса — отношение разности диаметров оснований к его высоте 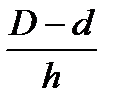= 2 tg α

При одном и том же угле конус­ность в 2 раза больше уклона. Перед размерным числом конусности наносят условный знак: ∆,вершину которого направляют в сторону вершины конуса. Порядок обозначения конусности по ГОСТ 2.307 — 68* показан на рисунке.

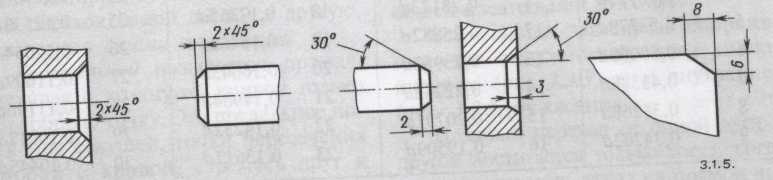
Этим же стандартом обусловлено обозначение размеров фасок под углом 45°. Размеры фасок под другими углами указывают по общим правилам — линейными и угловыми размерами или двумя линейными размерами.

Вопросы для самоконтроля

1. В каких случаях применяется сопряжение?

2. Какие виды сопряжения вы знаете?

3. Как обозначают на чертежах уклон и конусность?

4. Дайте определения лекальных кривых.

5. Раскройте принципы построения эллипса.

Раздел 2. Основы начертательной геометрии и проекционное черчение.

Т е м а 2.1. Методы проецирования

Методы проецирования. Плоскости и оси проекций, их обозначение, координаты точек. Проецирование точек, отрезков, плоских фигур.

При изучении темы необходимо усвоить терминологию процесса проецирова­ния, уяснить разницу между центральным и параллельным проецированием. Кроме вышесказанного для лучшего усвоения материала необходимо решить задачи на построение проекций точки, прямой, плоскости и их взаимного расположения.

Примем следующие обозначения элементов пространства. Точки будем обозначать прописными буквами латинского алфавита: А, В, С... или цифрами 1, 2, 3...; прямые — строчными буквами латинского алфавита: а, b, с..., а плоскости — прописными буквами греческого алфавита: Г, Л, П, S, Ф, Ґ, Q.

Между элементами пространства существуют следующие отношения.

Тождественность обозначается знаком ==, например А = В. Это обозначает, что точка А совпадает с точкой В.

Инцидентность (или принадлежность) обозначается знаком €. Например, А € а обозначает, что точка А принадлежит (инцидентна) прямой а.

Параллельность обозначается знаком ||. Например, K || L обозначает, что прямая К параллельна прямой.

Перпендикулярность обозначается знаком _|_. Например, a _|_ S обозначает, что прямая а перпендикулярна плоскости S.

Над элементами пространства можно выполнить операцию соединение, которую обозначают знаком и. Например, запись А и В ~ а обозначает, что в результате соединения точек А и В получена прямая а.

Операцию пересечение обозначают знаком ^. Запись т ^ n = К обозначает, что в результате пересечения прямых тип получена точка К.

1. Метод проекций

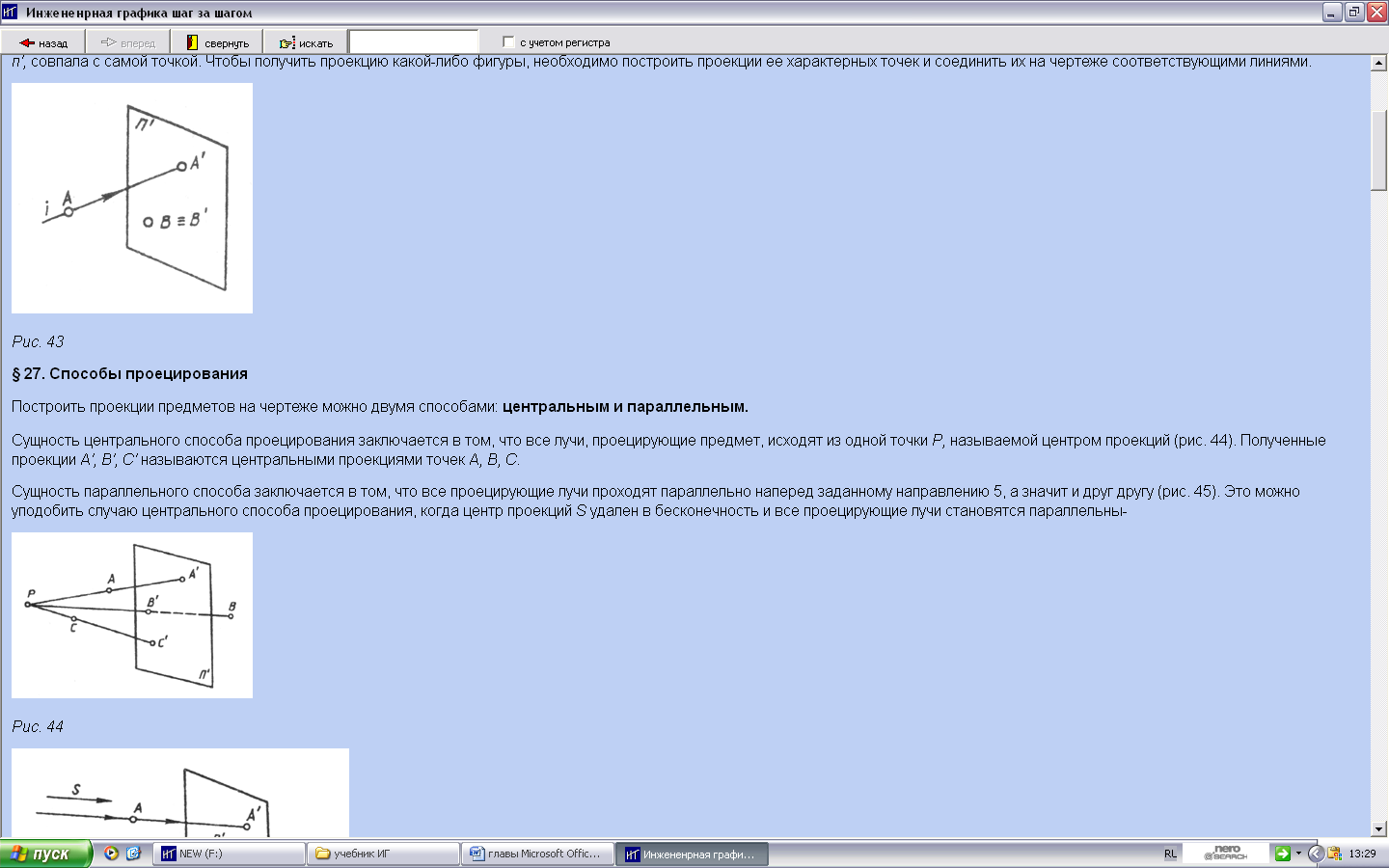
Теоретические свойства построения чертежа в инженерной графике базируются на правилах построения изображений, основанных на методе проекций. Изображение объектов трехмерного пространства на плоскости получают методом проецирования. Проецирование — это процесс, в результате которого получают изображения, представляющие собой проекции на плоскости.

Аппарат проецирования включает в себя изображаемые объекты — точки А, В, проецирующие лучи i и плоскость проекции п', на которой получается изображение объектов. Процесс проецирования заключается в проведении проецирующих лучей через заданные точки до встречи с плоскостью проекций. Точка пересечения проецирующего луча с плоскостью проекций и определяет проекцию этой точки. Так, проекцией точки А является точка А', т. е. [i ~ A; i ^ п' = А']. Проекцией точки В является точка В', хотя проекция точки В, лежащей в плоскости п', совпала с самой точкой.

Чтобы получить проекцию какой-либо фигуры, необходимо построить проекции ее характерных точек и соединить их на чертеже соответствующими линиями.

2. Способы проецирования

Построить проекции предметов на чертеже можно двумя способами:

ü центральным и

ü параллельным.

Сущность центрального способа проецирования заключается в том, что все лучи, проецирующие предмет, исходят из одной точки Р, называемой центром проекций. Полученные проекции А', В', С' называются центральными проекциями точек А, В, С.

Сущность параллельного способа заключается в том, что все проецирующие лучи проходят параллельно наперед заданному направлению S, а значит и друг другу. Это можно уподобить случаю центрального способа проецирования, когда центр проекций S удален в бесконечность и все проецирующие лучи становятся параллельными. При построении проекций А', В', С' этим способом они называются параллельными проекциями точек А, В, С.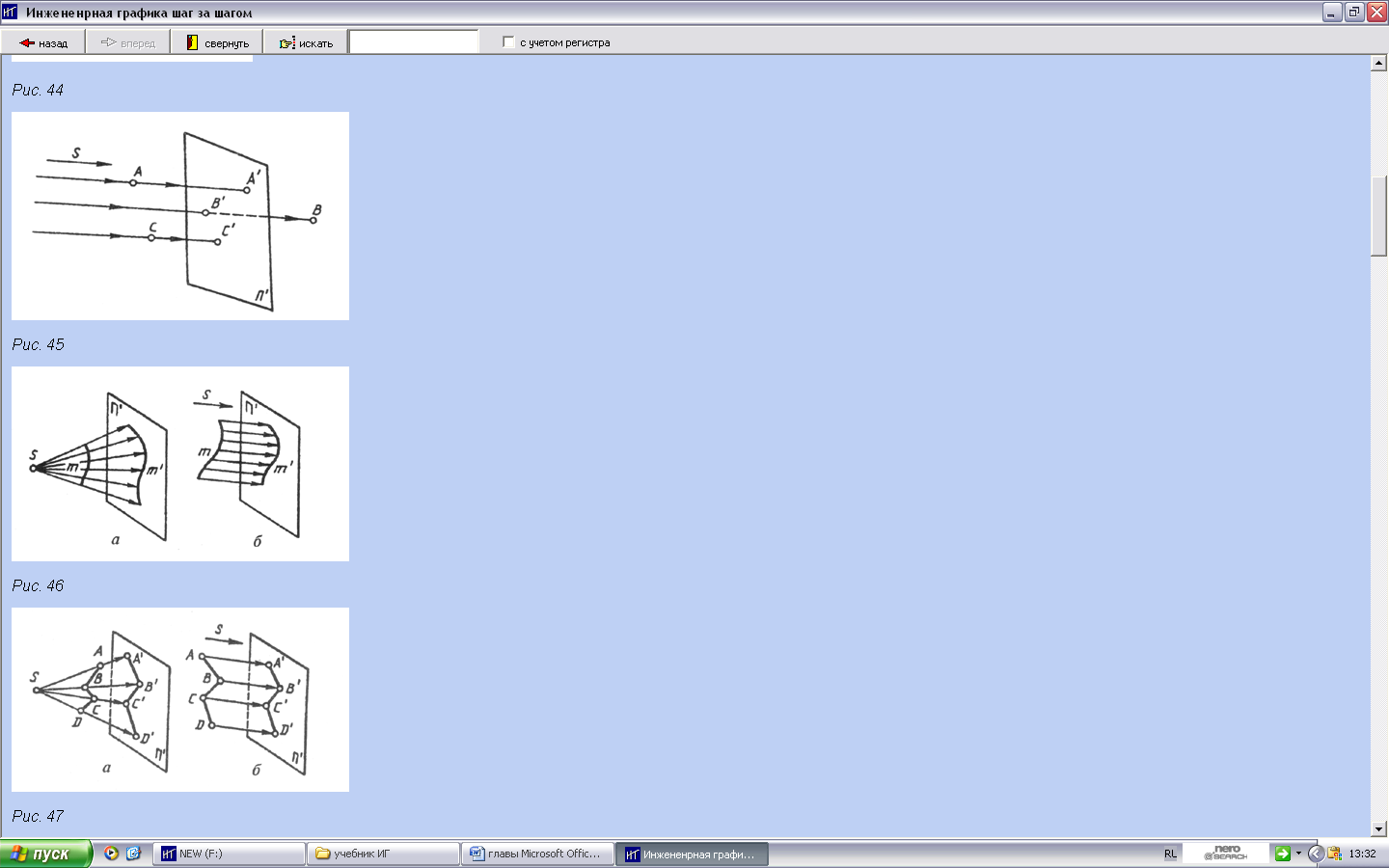

При проецировании совокупность проецирующих лучей образует различные геометрические фигуры. При проецировании прямой линии — это плоскость при проецировании ломаной линии — поверхность призмы или пирамиды, при проецировании кривой линии — коническая или цилиндрическая поверхность. В отличие от проецируемых фигур эти фигуры называют проецирующими.

3. Свойства проекций

Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.

Проекция точки есть точка.

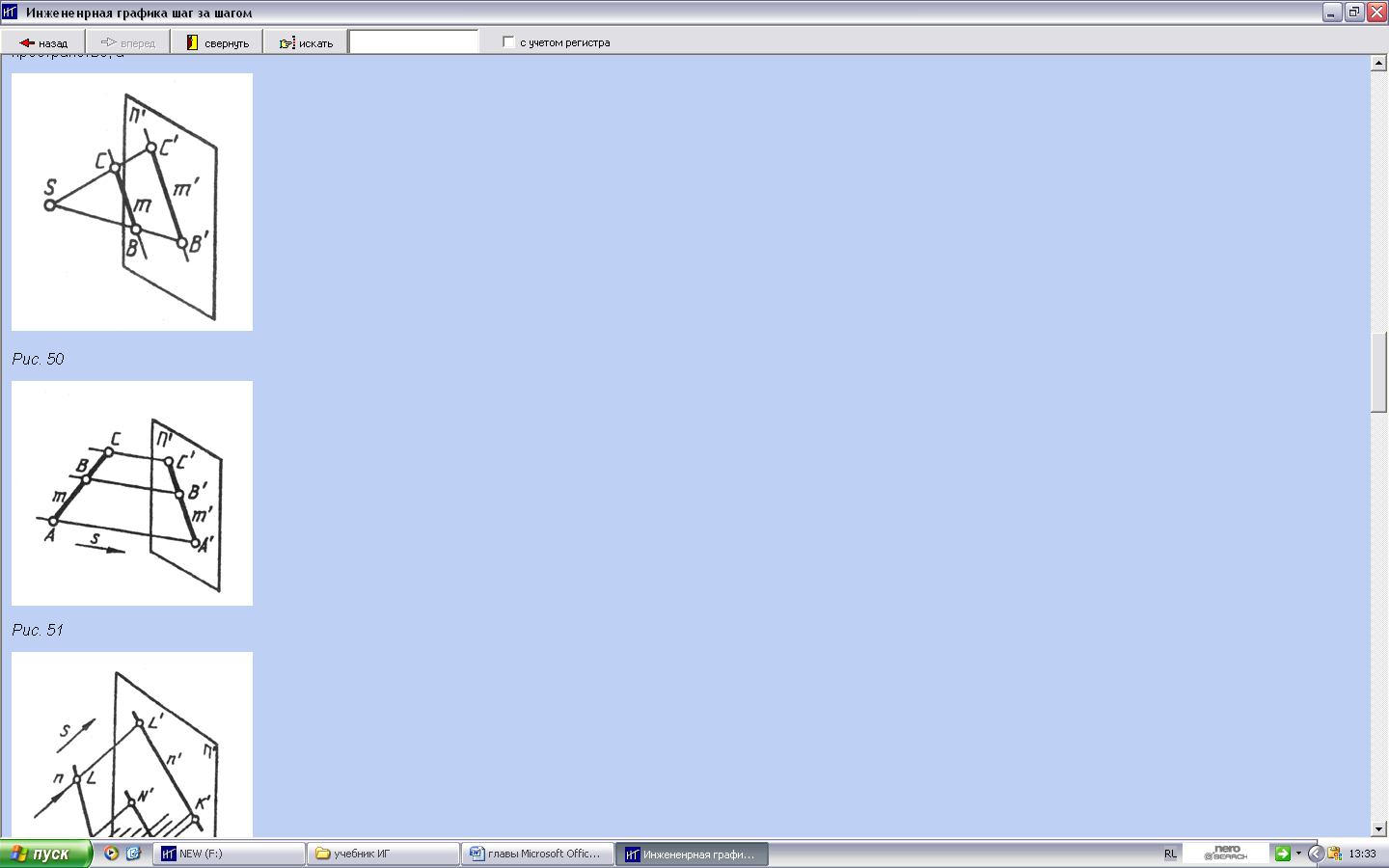Проекция прямой есть прямая. Проекция прямой определена, если известны проекции хотя бы двух ее точек. Если в пространстве прямая параллельна плоскости проекции п', то ее проекция параллельна самой прямой. При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.

При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций: АВ/ВС = А'В'/В'С.

При параллельном проецировании проекции параллельных прямых есть прямые параллельные. Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости Sm и Sn тоже будут параллельны. При пересечении их с плоскостью проекций п' получаем т'|| п'.

Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а их точки пересечения с плоскостью проекций п' — всю 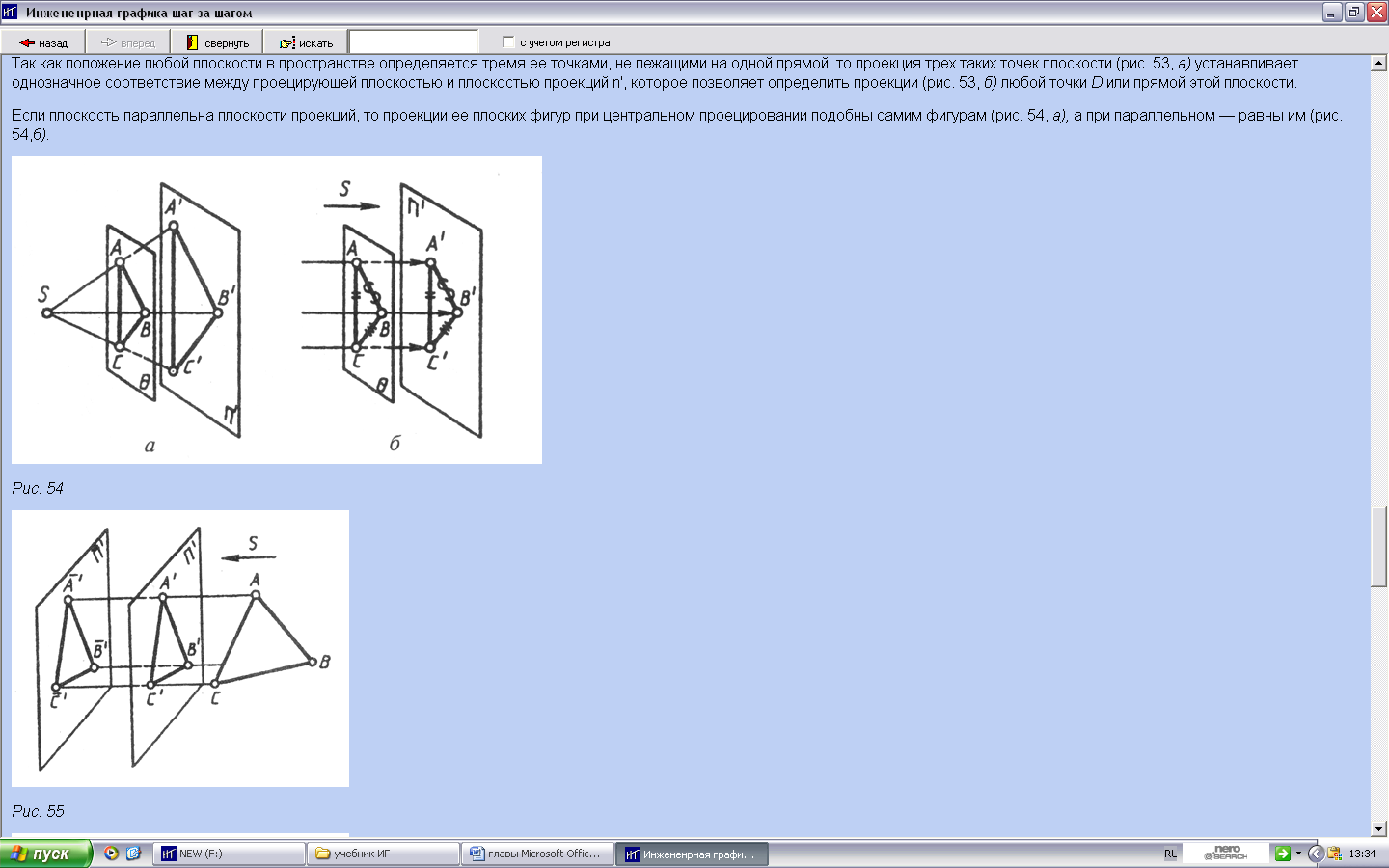плоскость проекций. Положение любой плоскости в пространстве можно задать тремя очками или двумя прямыми, принадлежащими ей, а также следами.

Прямые и плоскости (поверхности) могут занимать в пространстве проецирующее положение, если с ними совпадают проецирующие лучи.

Все эти геометрические фигуры можно рассматривать состоящими из проецирующих лучей, каждый из которых изображается точкой. Отсюда следует, что проекциями прямых, плоскостей, поверхностей, занимающих проецирующее положение, есть точки или линии их пересечения с плоскостью проекций («вырожденные» проекции).

4. Ортогональные проекции

Ортогональное (прямоугольное) проецирование есть частный случай проецирования параллельного, когда все проецирующие лучи перпендикулярны плоскости проекций. Ортогональным проекциям присущи все свойства параллельных проекций, но при прямоугольном проецировании проекция отрезка, если он не параллелен плоскости проекций, всегда меньше самого отрезка. Это объясняется тем, что сам отрезок в пространстве является гипотенузой прямоугольного треугольника, а его проекция — катетом: А'В' = AB cos α.

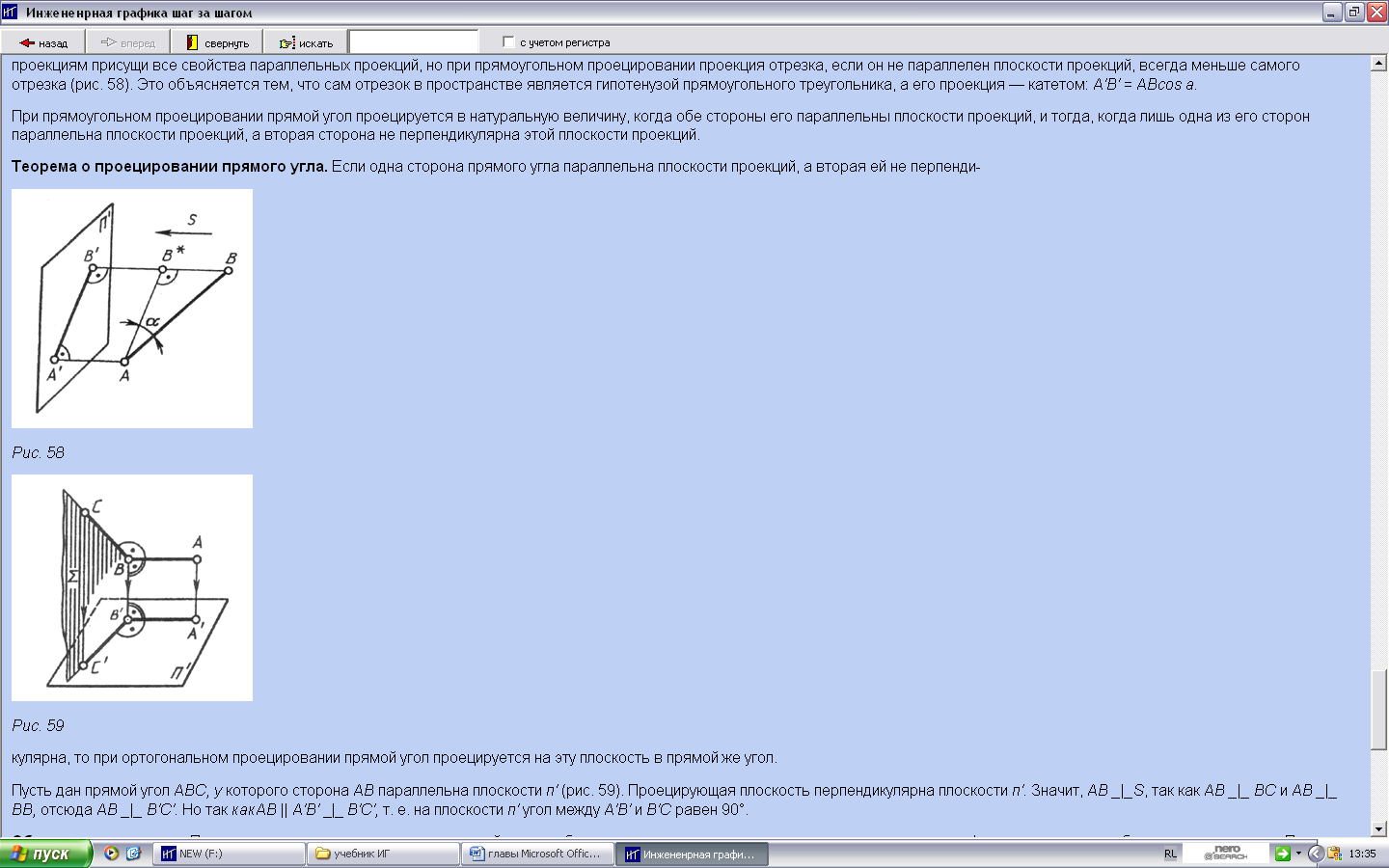При прямоугольном проецировании прямой угол проецируется в натуральную величину, когда обе стороны его параллельны плоскости проекций, и тогда, когда лишь одна из его сторон параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости проекций.

5. Обратимость чертежа.

Проецирование на одну плоскость проекций дает изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция точки не определяет положение самой точки в пространстве, так как не известно, на какое расстояние она удалена от плоскости проекций. Любая точка проецирующего луча, проходящего через заданную точку, будет иметь своей проекцией одну и ту же точку на плоскости проекций. Наличие одной проекции создает неопределенность изображения. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображение дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа.

6. Проекции точки

Рассмотрим основные принципы прямоугольного проецирования и способ получения ортогонального чертежа в системе трех плоскостей проекций. На рисунке показано расположение трех плоскостей проекций, с помощью которых получают ортогональный чертеж. Плоскости располагаются под углом 90° друг к другу.

Плоскость Н — горизонтальная плоскость проекций, плоскость V — фронтальная плоскость проекций, плоскость W — профильная плоскость проекций.

Линии пересечения плоскостей проекций называются осями проекций, или осями координат и обозначаются Ox, Oy, Oz. Точка пересечения трех осей координат (точка О) является началом координат, т. е. точкой, от которой ведется отсчет координат по осям Ox, Oy. Oz. Угол, образованный тремя плоскостями проекций, называют координатным углом, так как плоскости проекций являются базами отсчета расстояний (координат) и ограничи­вают пространство плоскостями проекций, в котором располагают проецируемые предметы.

Помещая изображаемый (проецируемый) предмет (геометрическая фигура, модель, деталь и т. п.) в определенное положение относительно плоскостей проекций V, Н и W, фиксируют его положение относительно этих плоскостей, что дает возможность получить взаимосвязанные изображения данного предмета, по которым легко представить его положение в пространстве, его форму. Каждое изображение (проекция) предмета на плоскость отображает то, что мы видим при взгляде на предмет в определенном направлении. Чтобы получить представление о форме предмета, обычно недостаточно рассмотреть предмет с какой-то одной стороны. Проецируя предмет в системе трех плоскостей проекций, его рассматривают с трех сторон, в направлениях, перпендикулярных трем плоскостям проекций.

Получив проекции предмета на трех плоскостях проекций, плоскости координатного угла развертывают в одну плоскость, как показано на рисунке. При этом плоскости Н и W условно разрезают по оси Оу, плоскость Н поворачивают вокруг оси Ох, а плоскость W — вокруг оси Oz, получают одну общую плоскость - плоскость чертежа. При этом ось Оу как бы разрезается пополам. Одна ее «половина» оказывается в плоскости Н и располагается перпендикулярно оси Ох, а другая — в плоскости W и располагается перпендикулярно оси Oz. Cовмещенные плоскости проекций разделяются взаимно перпендикулярными осями, которые определяют на чертеже рабочее поле для построения проекций предмета. Каждая плоскость проекций имеет два измерения по взаимно перпендикулярным направлениям. Для плоскости Н — это оси Ох и Оу, для плоскости V — оси Oz и Ох, для плоскости W- оси Oz и Оу₁.

Изображения, полученные на плоскостях координатного угла и совмещенные в одну плоскость, называют эпюром или ортогональным чертежом. Рассмотрим построение эпюра точки.

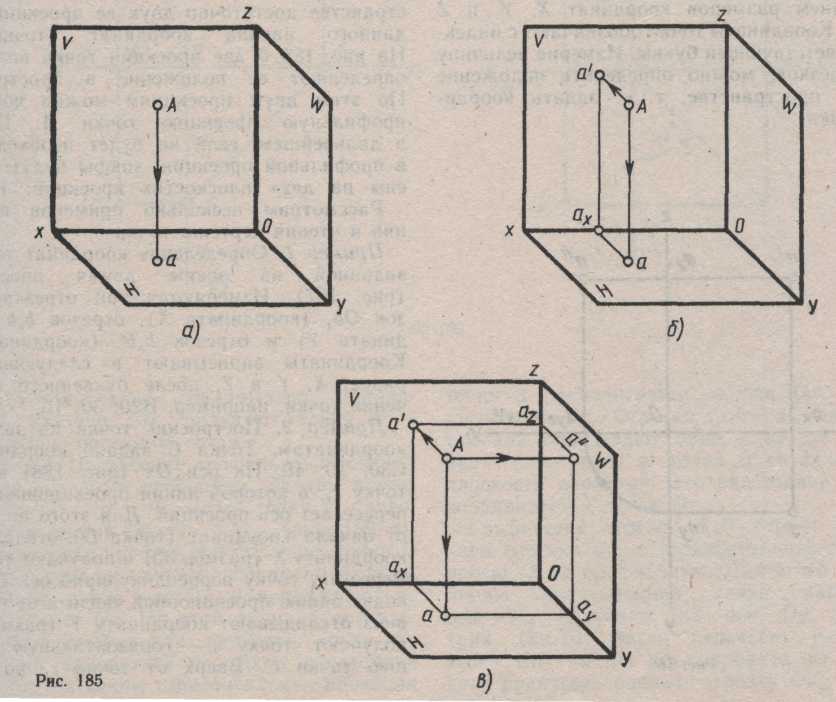
Проецирование точки на три плоскости проекций координатного угла начинают с получения ее изображения на плоскости Н — горизонтальной плоскости проекций. Для этого через точку А проводят проецирующий луч перпендикулярно плоскости Н. На рисунке перпендикуляр к плоскости Н параллелен оси Oz. Точку пересечения луча с плоскостью Н (точку а) выбирают произ­вольно. Отрезок Аа определяет, на каком расстоянии находится точка А от плоскости Н, указывая тем самым однозначно положение точки А на рисунке по отношению к плоскостям проекций. Точка а является прямоугольной проекцией точки А на плоскость Н и называется горизонтальной проекцией точки - А.

Для получения изображения точки А на плоскости V через точку А про­водят проецирующий луч перпендикулярно фронтальной плоскости проекций V. На рисунке перпендикуляр к плоскости V параллелен оси Оу. На плоскости Н расстояние от точки А до плоскости V изобразится отрезком аа_х, параллельным оси Оу и перпендикулярным оси Ох. Если представить себе, что проецирующий луч и его изображение проводят одновременно в направлении плоскости V, то когда изображение луча пересечет ось Ох в точке а_х, луч пересечет плоскость V в точке а'. Проведя из точки а_х в плоскости V перпендикуляр к оси Ох, который является изображением проецирующего луча Аа на плоскости V, в пересечении с проецирующим лучом получают точку а'. Точка а' является фронтальной проекцией точки А, т. е. ее изображением на плос кости V.

Изображение точки А на профильной плоскости проекций строят с помощью проецирующего луча, перпендикулярного плоскости W. На рисунке перпендикуляр к плоскости W параллелен оси Ох. Проецирующий луч от точки А до плоскости W на плоскости Н изобразится отрезком аа_у, параллельным оси Ох и перпендикулярным оси Оу. Из точки а_у параллельно оси Оz и перпендикулярно оси Оу строят изображение проецирующего луча аА и в пересечении с проецирующим лучом получают точку а". Точка а" является профильной проекцией точки А, т. е. изображением точки А на плоскости W. Точку а" можно построить, проведя от точки а' отрезок а'а₂ (изображение проецирующего луча Аа" на плоскости V) параллельно оси Ох, а от точки а _z— отрезок а"а_z парал­лельно оси Оу до пересечения с проецирующим лучом.

Получив три проекции точки А на плоскостях проекций, координатный угол развертывают в одну плоскость, как показано на рис. вместе с проекциями точки А и проецирующих лучей, а точку А и проеци­рующие лучи Аа, Аа' и Аа" убирают. Края совмещенных плоскостей проекций не проводят, а проводят только оси проекций Oz, Oy и Ох, Оу_х.

Дата добавления: 2014-11-26