
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
A) элементтері болса 10 страница
|
|
|
|
2. объединение, так же как и исходные минтермы, имеет координаты в виде последовательности независимых переменных 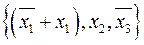 ,
,
3. аналитический результат склеивания (минимизированная функция рассматриваемого примера) получается путём логического перемножения координат полученного объединения единиц  .
.
Несмотря на свою простоту, пример 2.5.13 в основном отражает существо рассматриваемого метода минимизации логических функций. Усложнение практических задач минимизации обнаруживается в большем числе получающихся объединений и большем числе единиц, включаемых в объединения. Как следствие, появляются возможные альтернативы объединений. Для полноты описания метода, необходимо познакомиться с правилами организации объединения единиц и наметить критерий выбора объединений, соответствующих минимальной тупиковой форме функции.
Склеиваются только соседние минтермы, а объединяются только соответствующие им единицы, которые всегда оказываются рядом стоящими. Последнее отражает основную особенность карты Карно. Поэтому, объединять можно:
a) две рядом стоящие единицы,
b) две рядом стоящие пары единицы, образующие «четвёрку»
единиц,
c) две «четвёрки», объединяющие восемь единиц.
Конфигурация объединений строго регламентирована. Возможные её варианты представлены на рисунке 2.5.4.
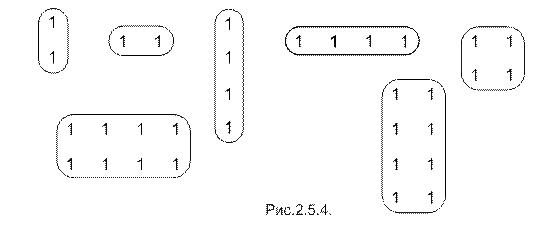
Существуют так же модификации разрешённых конфигураций объединений единиц (рисунок 2.5.5).
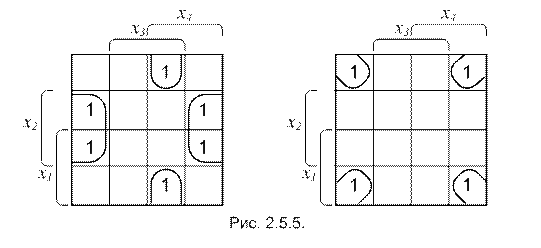
Действительно, если мысленно соединить верхний край карты с нижним, образовав трубочку или сделать то же самое с левым и правым краями карты, или, абстрагируясь от реальности, осуществить это всё одновременно, получим другие конфигурации объединений условно рядом стоящих единиц (рис. 2.5.5).
Два объединения на карте могут пересекаться. Допустимость пересечения объясняется возможностью размножить любую единицу в клетке карты. То есть, можно выделить для каждого объединения свою единицу (рис. 2.5.6). Возможность размножения единиц объясняется аксиомой 4 (п. 2.1).
 Пересечение объединений может быть однократным, двух, трёх, и четырёхкратным. Возможные варианты пересечения показаны на рисунке 2.5.7.
Пересечение объединений может быть однократным, двух, трёх, и четырёхкратным. Возможные варианты пересечения показаны на рисунке 2.5.7.

 Критерий выбора варианта объединения единиц на карте Карно из множества возможностей формулируется следующим образом. Для достижения минимальной тупиковой формы функции необходимо обеспечить:
Критерий выбора варианта объединения единиц на карте Карно из множества возможностей формулируется следующим образом. Для достижения минимальной тупиковой формы функции необходимо обеспечить:
1. минимум числа объединений единиц,
2. максимум единиц составляющих каждое объединение.
Первый пункт критерия носит безусловный характер. Второй пункт должен соблюдаться только при выполнении первого. Формулировку критерия сопровождают два следствия:
a) каждая единица на карте Карно должна принадлежать какому - либо объединению, даже если объединение содержит только одну единицу,
b) объединение должно содержать хотя бы одну «свою» единицу, не принадлежащую ни к какому другому объединению.
Эти следствия так же важно помнить при формировании вариантов объединений единиц.
Пример 2.5.14.
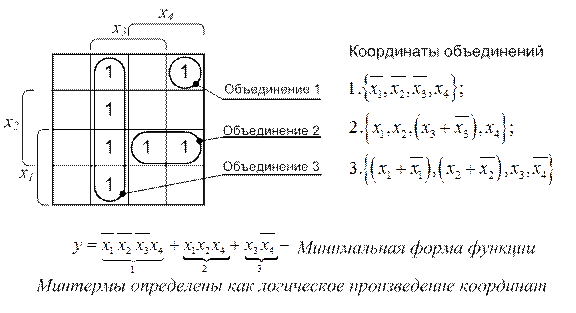
Составление аналитического вида минимизированной функции уже было показано в примере 2.5.13. Эти же действия для более сложного случая представлено в примере 2.5.14.
В процедуре минимизации функций обычно не расписывают действия как это сделано в примере 2.5.14. Можно сразу же составлять минтермы, не включая в них координаты заключённые в скобки.
Пример 2.5.15.

Карты Карно для пяти переменных в части формирования объединений имеют специфику. Единицы, находящиеся только в левой половине карты или только в правой половине карты, объединяются точно так же, как это делается на картах для четырёх переменных. Единицы, находящиеся в разных половинах карты, считаются рядом стоящими и, следовательно, подлежат объединению, если при сгибе карты по вертикальной средней линии они будут накладываться друг на друга. Если всё же возникает сомнение по поводу близости единиц, всегда можно получить по карте соответствующие им минтермы и оценить соседние они или нет.
Пример 2.5.16.
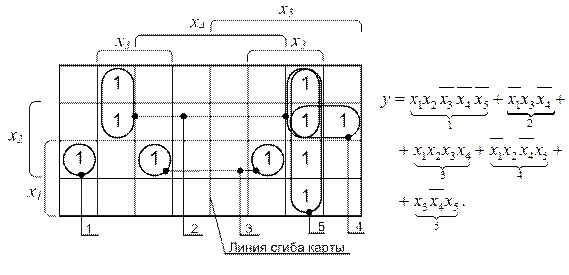
Наглядность формирования объединений на карте Карно для функций шести переменных практически пропадает. Поэтому, метод минимизации с использованием карт Карно практически полезен для функций до четырёх и иногда до пяти переменных. 
В своей основе, аналогичен методу минимизации логических функций с использованием карт Карно. Матрица, по сути дела, есть та же карта Карно, но с иной системой расстановки границ переменных. Границы размечаются по правому и нижнему краям матрицы. Система разметки чётко определена и легко запоминается. Разметка начинается с правого края матрицы. Нижняя половина матрицы образует зону для 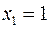 и обозначается
и обозначается 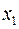 . Верхняя половина соответствует зоне
. Верхняя половина соответствует зоне 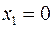 . Нижняя половина каждой исходной половины выделяется для
. Нижняя половина каждой исходной половины выделяется для 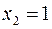 и обозначается
и обозначается 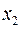 . Оставшиеся половины определяют
. Оставшиеся половины определяют 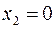 . Такая разбивка продолжается до тех пор, пока ширина зоны не станет равной высоте клетки матрицы. Нижний край матрицы разбивается точно так же, начиная со следующей переменной. Такую систему расстановки границ матрицы для функций с числом независимых переменных
. Такая разбивка продолжается до тех пор, пока ширина зоны не станет равной высоте клетки матрицы. Нижний край матрицы разбивается точно так же, начиная со следующей переменной. Такую систему расстановки границ матрицы для функций с числом независимых переменных 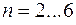 можно увидеть на рисунке 2.5.8.
можно увидеть на рисунке 2.5.8.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 1774; Нарушение авторских прав?; Мы поможем в написании вашей работы!