A) элементтері болса 6 страница

Пример 2.3.4.

Конъюнкция любого числа элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ).

Пример 2.3.5.

;

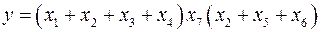ДНФ, в которой каждая элементарная конъюнкция содержит все переменные, называется совершенной дизъюнктивной нормальной формой (СДНФ).

Пример 2.3.6.

КНФ, в которой каждая элементарная дизъюнкция содержит все переменные, называется совершенной конъюнктивной нормальной формой (СКНФ).

Пример 2.3.7.

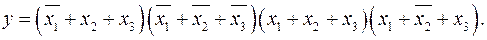
2.4 Преобразование функций алгебры логики

в СДНФ и СКНФ.

В пункте 1.6.1 с помощью теоремы (1.4) была показана возможность представлять любую функцию общей алгебры логики в базисе {И, ИЛИ, НЕ}. Можно использовать ту же самую теорему, чтобы доказать более сильное утверждение: любую функцию алгебры логики можно представить в СНДФ и СКНФ. Для доказательства используем две аналитические формулировки этой теоремы.

(2.20)

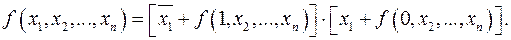
(2.21)

Справедливость этой теоремы доказывается путём подстановк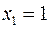и и 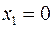. В результате предлагаемой подстановки (2.20) и (2.21) превращаются в тождества и, тем самым, доказывая справедливость этих равенств. Правая часть (2.20) и (2.21) есть результат разложения функции по переменной 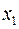. В свою очередь, полученный результат можно дополнительно разложить по переменной 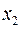. Если такую процедуру довести до конечного разложения по переменной 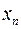, получим СДНФ и СКНФ. Для функции трёх переменных рассматриваемое разложение в СДНФ принимает вид (2.22) 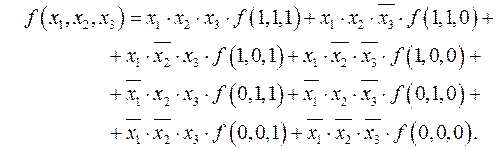(2.22)

Такое же разложение, но в СКНФ по (2.21), представляет (2.23).

(2.23)

Естественно, что (2.22) будут составлять только те логические слагаемые, для которых 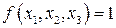(согласно аксиоме 7), а, в (2.23) останутся только те логические сомножители, для которых 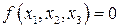(согласно аксиоме 2).

Представим рассматриваемую функцию в табличной форме (табл. 2.4.1). Совместный визуальный анализ этой таблицы с (2.22),

Таблица 2.4.1
№	x1	x2	x3

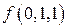
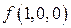
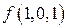
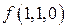
затем, с (2.23) даёт возможность сформулировать правило преобразования табличной формы представления логической функции в СДНФ и СКНФ.

Для получения СДНФ необходимо выполнить следующие действия.

1) Выделить строки таблицы истинности, для которых функция имеет значение «1» (истина). Каждой выделенной строке будет соответствовать логическое слагаемое (минтерм) СДНФ.

2) Построить каждое логическое слагаемое СДНФ в виде логического произведений полного набора логических переменных 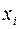. Причём, в таком произведении 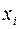лагаемыеических произведений полного набора логических переменныхоторыхзаписывается в прямой форме (то есть 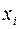), если в левой части таблицы (в строке соответствующей рассматриваемому слагаемому) 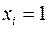. Иначе, 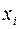записывается в инверсной форме (то есть), если .

Для получения СКНФ необходимо выполнить следующие действия.

1) Выделить строки таблицы истинности, для которых функция имеет значение «0» (ложь). Каждой выделенной строке будет соответствовать логический сомножитель (элементарная дизъюнкция) СКНФ.

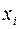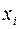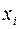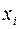2) Построить каждый логический сомножитель СКНФ в виде лоческой суммы полного набора логических переменных . Причём, в такой сумме записывается в прямой форме (то есть ), если в левой части таблицы (в строке соответствующей рассматриваемому сомножителю) . Иначе, записывается в инверсной форме (то есть ), если .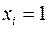

Пример 2.4.1.

x1	x2	x3	y
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Пусть задана функция в табличной форме.

Тогда

СДНФ функции: ,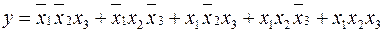

СКНФ функции: .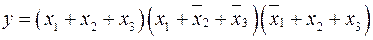

Справедливость полученных результатов может быть проверена обратным преобразованием.

Преобразование логической функции общего вида в СДНФ и СКНФ производится двумя способами. Функцию можно преобразовать в табличную форму и, затем, в соответствии с предлагаемым правилом сформировать СДНФ (СКНФ).

Пример 2.4.2.

Задана функция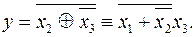

Надо преобразовать её в СДНФ.

x3	x2	x1			a		b		x3	y
			1	1	1	0	1	0	0
			1	1	1	0	1	0	0
			0	1	0	1	0	1	0
			0	1	0	1	1	0	0
			1	0	0	1	1	0	0
			1	0	0	1	1	0	0
			0	0	1	0	0	1	1
			0	0	1	0	1	0	0

В соответствии с рангами операций проведём последовательное преобразование функции в табличную форму. Обозначим

Дата добавления: 2014-11-09