A) элементтері болса 2 страница

В алгебре логики число функций с n переменными конечно и однозначно зависит от n. Оно определяется числом возможных сочетаний нулей и единиц в последнем столбце таблицы истинности соответствующем значениям функции. Отсюда вытекает, что полное число возможных функций n переменных равно N(n) = 2^M(n), где M(n) = 2ⁿ – число строк таблицы.

Любую функцию алгебры логики для n > 2 можно выразить с помощью функций двух переменных. Например,

y = f (x₁, x₂, x₃) = g (z, x₃), где z = φ (x₁, x₂).

Поэтому, в алгебре логики детально рассматриваются только функции одной и двух переменных. Через наборы данных функций выражаются все остальные функции для любого числа переменных.

1.3.Логические функции одной переменной.

Число функций одной переменной равно 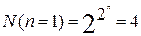. Эти функции в табличной форме определяются следующим образом.

Таблица 1.3.1.
x	yo		x	y1		x	y2		x	y3

Для общего обзора всех функций лучше воспользоваться более компактной формой совмещённого представления таблиц (табл. 1.3.2).

Таблица 1.3.2.
x	y0	y1	y2	y3

Каждая из функций таблицы имеет название и определённое аналитическое представление.

y ₀ – «нулевая функция» или «константа нуля», y₀ = 0.

y ₁ – «инверсия» или операция «НЕ», y ₁ = , читается «НЕ ».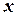

y ₂ – функция «повторение», y ₂ = .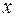

y ₃ – «единичная функция» или «константа единицы», y₃ = 1.

Число функций двух переменных равно . Совмещённая таблица истинности для этих шестнадцати функций имеет вид.

Таблица 1.4.1.

x2

x1

y0

y1

y2

y3

y4

y5

y6

y7

y8

y9

y10

y11

y12

y13

y14

y15

Таблица легко строится. Для этого надо иметь в виду особенность чередования нулей и единиц по строчкам в правой её части.

Функции двух переменных, представленные в таблице 1.4.1, так же как функции одной переменной, имеют названия. Для них тоже используются определённые индивидуальные значки операций. Исторически сложилось так, что некоторые из функций имеют два и более названий. То же самое получается и со значками операций. При описании функций будем отмечать это обстоятельство.

y ₀ – «нулевая функция» или «константа нуля», y ₀ = 0.

y ₁ – «стрелка Пирса», у ₁ = x ₁ x ₂.

y ₂ – «запрет x ₂», y ₂ = x ₁ x ₂.

y ₃ – «инверсия x ₂», y ₃ = 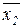; (переменная x ₁ для этой функции

фиктивна).

y ₄ – «запрет x ₁», y ₄ = x ₂ x ₁.

y ₅ – «инверсия x ₁», y ₅ = 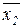; (переменная x ₂ для этой функции фиктивна).

y ₆ – «неэквивалентность» или «сложение по модулю 2»,

y ₆ = x ₁ 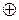x ₂.

y ₇ – «штрих Шеффера», y ₇ = x ₁ / x ₂.

y ₈ – «конъюнкция» или «операция И» или «логическое умножение»,

y ₈ = x ₁ 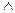x ₂ = x ₁· x ₂ = x ₁ x ₂.

y ₉ – «эквивалентность» или «равнозначность», y ₉ = x ₁ x ₂.

y₁₀ – «повторение x ₁», y₁₀ = x ₁, (переменная x ₂ для этой функции фиктивна).

y₁₁ – «импликация x ₁», y ₁₁ = x ₂ 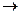x ₁.

y₁₂ – «повторение x ₂», y₁₂ = x ₂, (переменная x ₁ для этой функции фиктивна).

y₁₃ – «импликация x ₂», y ₁₃ = x ₁ 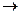x ₂.

y₁₄ – «дизъюнкция» или «операция ИЛИ» или «логическое сложение», y₁₄ = x ₁ x ₂ = x ₁ + x ₂.

y₁₅ – «единичная функция» или «константа единицы»,

y₁₅ = 1.

Не все из перечисленных функций реализуют логические операции, обладающие новизной. Так, из таблицы 1.4.1 легко обнаруживаются равенства.

; ; ; ;

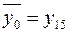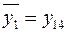; ; ; ; (1.1)

; ; ; ;

; ; ; .

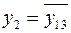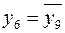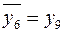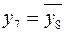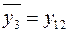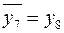То есть, только половина функций может обладать существенной новизной. Кроме того, y ₀ и y₁₅ есть константы. Они были введены функциями одной переменной. Выражения для y ₃, y ₅, y₁₀ и y₁₂ по существу (это вытекает из таблицы 1.4.1) так же являются функциями одной переменной. В итоге получается, что функций двух переменных по видам логического преобразования обладают избыточностью.

Равенства (1.1) дают интересные и важные соотношения. О них мы не раз будем упоминать в дальнейшем. В частности, расшифровка равенств и 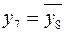даёт выражения

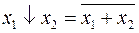, (1.2)

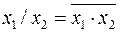(1.3)

часто используемые в процессе преобразования функций. Попутно заметим, что данные выражения позволяют называть функцию «стрелка Пирса» операцией «ИЛИ – НЕ», а функцию «штрих Шеффера» – операцией «И – НЕ».

1.5. Сложные логические функции. Ранги операций.

Простыми называются логические функции реализуемые с помощью только одной логической операции.

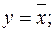
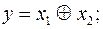
Если число операций два или более, функцию условно называют сложной.

Заметим, сложными могут быть функции с малым числом переменных (одно, два).

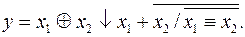
Сложные логические функции будут определены, если известен порядок выполнения логических операций. В алгебре логики такой порядок принят. Он объявлен в форме ранга операций:

Дата добавления: 2014-11-09