
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
A) элементтері болса 1 страница
|
|
|
|
A).
A) -2
3.2 Логика релейно-контактных схем.
2.5.7. Минимизация систем логических функций.
2.5.4. Матричный метод минимизации логических функций.
2.5.2. Карты Карно.
2.5. Минимизация логических функций.
2.3. Формы представления логических функций.
2.2 Двойственность логических функций.
1.7. Частные алгебры логики.
1.6.5. Базис { / }.
1.6.3. Базис {И, НЕ}.
1.6.2. Базис {ИЛИ, НЕ}.
1.6.1. Базис {И, ИЛИ, НЕ}.
1.6. Функционально полные системы операций.
1.4. Логические функции двух переменных.
1.2. Логические функции. Общие сведения.
1.1. Логические переменные.
В алгебре логики логической переменной (логической величиной) является высказывание, которому может быть присвоено значение «истина» (true) или «ложь» (false). По своей сути высказывания весьма разнообразны. Например:
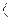 Число А делится на 4
Число А делится на 4  ;
;
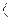 Студент Петров учится на 2-ом курсе
Студент Петров учится на 2-ом курсе  ;
;
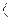 X > 2
X > 2  ;
;
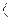 Электродвигатель вентилятора включён
Электродвигатель вентилятора включён  ;
;
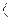 Y + 3 = Z - 8
Y + 3 = Z - 8 
и так далее. Высказывание может быть представлено в форме приказа выполнить определенное действие.
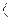 Дать питание на катушку реле Р3
Дать питание на катушку реле Р3  ;
;
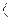 Открыть клапан подачи воды в расходный бак
Открыть клапан подачи воды в расходный бак 
и тому подобное.
Логическая переменная, как и в обычной алгебре, обозначается буквой, буквой с индексом, буквой и цифрой: x, x4, x4, y13, gk, bkn. Первой в идентификаторе переменной должна стоять буква.
x2 = 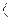 На улице светит солнце
На улице светит солнце  ;
;
a3 = 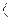 Сработала максимальная защита по току
Сработала максимальная защита по току  .
.
Как уже было сказано, логическая переменная может принимать только два значения «истина» или «ложь». Для сокращения записи «истина» обозначается знаком «1», а значение «ложь» - «0». Знаки «1» и «0» в данном случае рассматриваются не как цифры, а лишь как символы, отражающие указанное обозначение. Например, пусть
x = 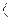 На улице идет дождь
На улице идет дождь  .
.
Могут быть два варианта. Либо это так и x = 1. В противном случае x = 0. Другой пример.
y = 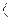 Z < 3
Z < 3  .
.
y = 1 при Z = 2, y = 0 при Z = 5.
Существуют высказывания, которые всегда имеют значение «истина» или значение «ложь».
h = 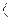 Земля – планета солнечной системы
Земля – планета солнечной системы  ;
;
s = 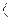 Sin2
Sin2 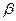 + Cos2
+ Cos2 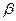
 1
1  .
.
Здесь всегда h = 1, а s = 0. Они называются соответственно «константа единицы» и «константа нуля».
Приведенные выше логические переменные являются простыми высказываниями. В общем случае высказывания могут быть сколь угодно сложными. Например,
x12 = 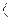 d > 1, g < 0, v = 8
d > 1, g < 0, v = 8  .
.
Такое высказывание выражается через простые высказывания
b1 = 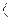 d >1
d >1  , b2 =
, b2 = 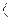 g < 0
g < 0  , b3 =
, b3 = 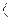 v = 8
v = 8 
являющиеся аргументами некоторой логической функции, образованной с помощью определённого набора логических операций. Логическим операциям и логическим функциям посвящены следующие параграфы.
Соотношения между логическими переменными в рассматриваемой алгебре выражаются в форме логических функций. Общий вид логической функции представляется таким же образом, как это делается в обычной алгебре.
y = f (x1, x2, x3, … xn). 
Задание конкретной функции может осуществляться в табличной и аналитической формах. Описание аналитической формы отложим до следующего параграфа. Сейчас остановимся на табличной форме.
| Таблица 1.2.1. | |||
| x3 | x2 | x1 | y |
Таблица представляющая функцию состоит из двух частей. В первой части записываются все возможные сочетания значений независимых переменных. Правая часть отводится для значений функции соответствующих каждому сочетанию значений независимых аргументов. Примером табличной записи конкретной функции трёх переменных x1, x2, x3 служит следующее представление (табл. 1.2.1). Такая таблица имеет название « таблица истинности ». Отметим некоторые параметры конфигурации таблицы и правила её составления.
Число возможных сочетаний значений n независимых переменных равно 2n. Для приведённого примера (табл. 1.2.1) n = 3 и, следовательно, число строк составляет 23 = 8. Столбцы для независимых переменных заполняются по строкам значениями этих переменных «0» и «1» с различным периодом их следования. Для x1 периодом будет (0-1). Для x2 – (0-0-1-1). Для x3 – (0-0-0-0-1-1-1-1). То есть, для каждой последующей переменной число нулей и единиц в периоде удваивается.
| Таблица 1.2.2. | |||
| x1 | x2 | x3 | y |
| Таблица 1.2.3. | |||
| x3 | x2 | x1 | y |
Порядок следования независимых переменных в таблице может быть любым. При изменении порядка меняются местами лишь строки таблицы. Рассматриваемая функция (табл. 1.2.1) при обратном порядке расстановки переменных формально представляется таблицей 1.2.2..
| Таблица 1.2.4. | ||
| x3 | x2 | y |
Логическая функция может включать переменные, от которых она не зависит. Такие переменные называются фиктивными. Они могут быть удалены из таблицы истинности. В результате получается тождественная логическая функция. Примером может служить функция заданная таблицей 1.2.3. Заметим, что в первых двух строках таблицы при изменении значения только x1 значение функции y не меняется. Тоже самое можно видеть и для остальных пар строчек. Получается, что y зависит только от x2 и x3. В зтом случае рассматриваемую функцию можно представить (табл. 1.2.4.) в виде таблицы истинности, которая не включает x1.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 1344; Нарушение авторских прав?; Мы поможем в написании вашей работы!