A) элементтері болса 5 страница

Из особенностей логических переменных и аксиом вытекают некоторые закономерности, которые представляются как законы алгебры. Для булевой алгебры выявлены следующие соотношения, которые рассматриваются как законы.

1. Переместительный закон.

1.1. 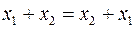; (2.1)

1.2. 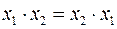. (2.2)

2. Сочетательный закон.

2.1. 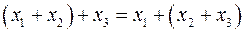; (2.3)

2.2. 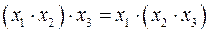. (2.4)

3. Распределительный закон.

3.1. 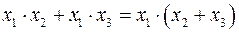; (2.5)

3.2. 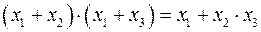. (2.6)

Обе формы первого и второго закона и первая форма третьего закона (2.1, 2.2, 2.3, 2.4, 2.5) очевидны и особого доказательства не требуют. Остановимся лишь на (2.6).

,

что и требовалось доказать. В процессе доказательства использовались закон (2.5) и 4-ая и 7-ая аксиомы.

4. Закон поглощения.

4.1 . (2.7)

Следствие: 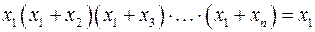. (2.8)

4.2 . (2.9)

Следствие: 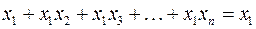. (2.10)

Доказательство (2.7):

.

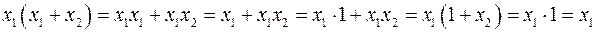Здесь содержится доказательство и для (2.9).

5. Закон склеивания.

5.1 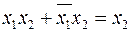; (2.11)

5.2 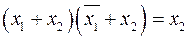. (2.12)

Доказательство (2.11):

.

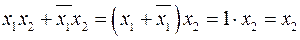Доказательство (2.12):

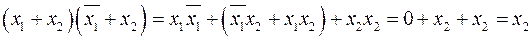6. Закон обобщённого склеивания.

6.1 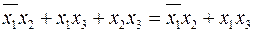; (2.13)

6.2 . (2.14)

Доказательство (2.13):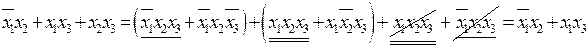

Доказательство (2.14).

Раскроем скобки сначала левой части равенства (2.14) а, затем, правой его части.

;

.

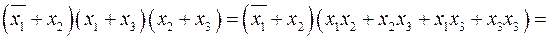
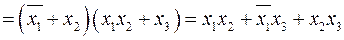Результаты преобразований одинаковы, что подтверждает справедливость (2.14).

7. Закон без имени.

7.1 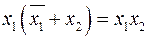; (2.15)

7.2 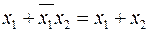. (2.16)

Доказательство (2.15):

.

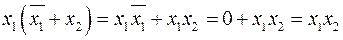Доказательство (2.16).

Развернём 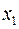с помощью действия обратного склеиванию (см. 2.11).

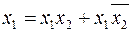, тогда

.

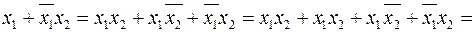
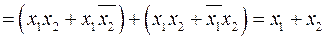8. Закон де Моргана.

8.1. ; (2.17)

8.2. 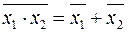. (2.18)

Доказательство (2.17) и (2.18) заключается в сравнивании табличных форм левых и правых частей этих равенств. Данный закон имеет обобщённую форму.

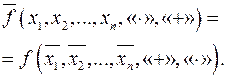
8.3. (2.19)

Равенство (2.19) означает следующее. Отрицание функции равно самой функции с отрицанием переменных. Порядок выполнения операций сохраняется, а сами операции меняются с «И» на «ИЛИ» и с «ИЛИ» на «И».

Пример 2.1.1.

.

Чтобы сохранить при преобразовании порядок выполнения операций в правой части равенства использовались скобки.

Функция 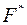называется двойственной по отношению к функции 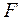, если 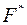образуется из 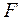путем замены операций «И» на операцию «ИЛИ» и операций «ИЛИ» на операцию «И». Функцию 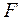будем называть оригиналом. Порядок выполнения операций в двойственной функции должен сохраняться таким, каким он был в оригинале.

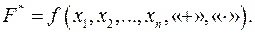
Пример 2.2.1.

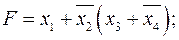
Для недопущения возможных ошибок при написании двойственной формы функций, рекомендуется в оригинале предварительно расставить скобки, дополнительно учитывающие ранги операций. Затем, в полученной двойственной форме, скобки, не изменяющие порядок выполнения операций, удаляются.

Пример 2.2.2.

.

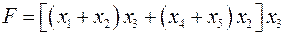Расставляем дополнительные скобки, не меняющие формулу.

.

Делаем преобразование в двойственную форму.

.

Убираем ненужные скобки и получаем окончательный вид двойственной функции

.

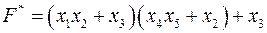Двойственные функции обладают следующими свойствами.

1. Если имеются две тождественно равные функции 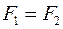, то их двойственные формы также равны .

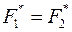2. Если 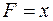, то 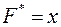. Свойство подтверждается следующим образом.

; .

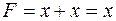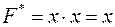3. Если , то 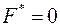. Действительно, так как 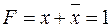(согласно пятой аксиоме), то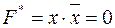 (согласно девятой аксиоме).

4. Если 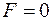, то 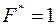. Например, если 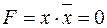, то .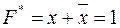

Эти свойства бывают очень полезны в тех случаях, когда преобразование логических выражений в двойственном виде делать удобнее, чем в оригинале.

Примером двойственных функций можно считать все вторые формы законов булевой алгебры, если принять первые формы за оригиналы.

Форма логических функций представленных в базисе {И, ИЛИ, НЕ} называется нормальной.

Пример 2.3.1.

.

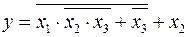Очень важным является более узкий класс функций со структурой, образованной элементарными составляющими двух типов: элементарных конъюнкций и элементарных дизъюнкций.

Элементарной конъюнкцией k- того ранга или, иначе, минтермом k- того ранга называется логическое произведение k логических переменных, каждая из которых может быть представлена в прямом или инверсном виде.

Пример 2.3.2.

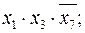
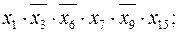
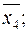
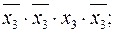
Замечание: конъюнкци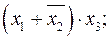и не являются элементарными

Элементарной дизъюнкцией называется логическая сумма любого числа логических переменных, каждая из которых может быть представлена в прямом или инверсном виде.

Пример 2.3.3.

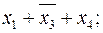
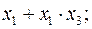
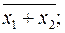
Замечание: дизъюнкции не являются элементарными.

Дизъюнкция любого числа элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).

Дата добавления: 2014-11-09