
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
A) элементтері болса 11 страница

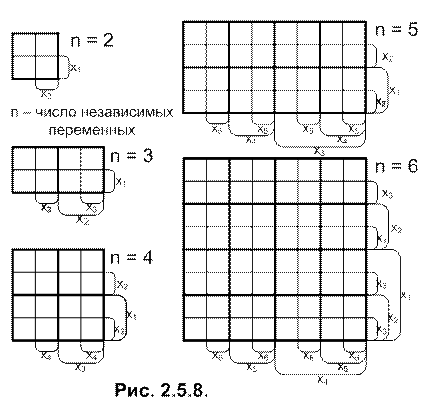 Другая особенность матрицы проявляется в соответствии её клеток со строчками таблицы истинности. Если в таблице истинности принят порядок расстановки переменных
Другая особенность матрицы проявляется в соответствии её клеток со строчками таблицы истинности. Если в таблице истинности принят порядок расстановки переменных 
 , номера строк таблицы совпадает с номерами клеток матрицы для функций с любым числом переменных. Эта особенность позволяет легко преобразовывать таблицу истинности в матричную форму представления функции (рис. 2.5.9).
, номера строк таблицы совпадает с номерами клеток матрицы для функций с любым числом переменных. Эта особенность позволяет легко преобразовывать таблицу истинности в матричную форму представления функции (рис. 2.5.9).
Изменение системы расстановки границ переменных на матрицах, по сравнению с картами Карно, меняет способ образования объединений единиц при минимизации функций. Матрица разбивается на квадраты различного уровня общности. Их назвали квадратами 1-ого ранга, 2-ого ранга, 3-его ранга и так далее. Квадрат 1-ого ранга содержит четыре клетки матрицы. Квадрат 2-ого ранга содержит четыре квадрата 1-ого ранга. Квадрат 3-его ранга содержит четыре квадрата 2-ого ранга и так далее (рис. 2.5.10).
 В соответствии с законом склеивания (2.11), объединению подлежат единицы, соответствующие соседним минтермам. Соседство обнаруживается следующим образом. В квадратах 1-ого ранга это рядом стоящие единицы. В квадратах 2-ого ранга соседство минтермов обнаруживается по совпадению их единиц при наложении друг на друга только рядом стоящих квадратов 1-ого ранга. Эта операция проводится для каждого квадрата 2-ого ранга, считая его изолированным. Возможность объединения единиц в рамках квадратов следующих рангов определяется аналогично.
В соответствии с законом склеивания (2.11), объединению подлежат единицы, соответствующие соседним минтермам. Соседство обнаруживается следующим образом. В квадратах 1-ого ранга это рядом стоящие единицы. В квадратах 2-ого ранга соседство минтермов обнаруживается по совпадению их единиц при наложении друг на друга только рядом стоящих квадратов 1-ого ранга. Эта операция проводится для каждого квадрата 2-ого ранга, считая его изолированным. Возможность объединения единиц в рамках квадратов следующих рангов определяется аналогично.
Условно, минимизацию логических функций можно разделить на два этапа. На первом из них производится построение всех возможных объединений единиц. Объединения наращиваются постепенно, по мере перехода от квадратов q -того ранга к квадратам (q – 1)-ого ранга. Если в квадрате q -того ранга для какой-либо единицы не нашлось пары, считается, что данная единица сама составляет объединение. При наращивании объединений, рядом стоящими следует считать не только совпадающие единицы, но и совпадающие объединения единиц. На первом этапе минимизации руководством к действию является критерий максимум единиц в каждом объединении.
Второй этап минимизации состоит в анализе полученных объединений. Цель анализа - выявить объединения, в которых все без исключения единицы принадлежат так же к другим объединениям, пересекающимися с анализируемым. Такие объединения являются претендентами на возможное исключение из общего состава полученных объединений (речь идёт об исключении самого факта объединения, а не единиц в него входящих). Претендентов на исключение может быть несколько. Решать вопрос об исключении каждого из них надо делать последовательно. Это связано с тем, что исключение одного претендента может привести к изменению состава других претендентов. В общем случае такая процедура многовариантна. Критерием выбора минимального варианта логической функции – минимум общего числа объединений единиц.
Пример 2.5.17.
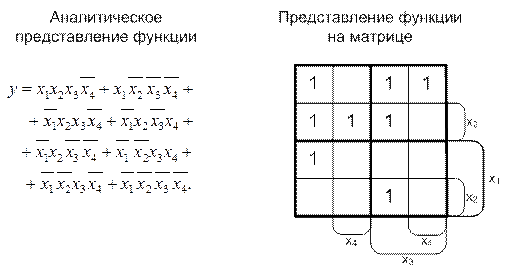
Пример 2.5.18.
Требуется минимизировать функцию, заданную в примере 2.5.17.

Процедура минимизации функции в примере 2.5.18 расписана по шагам, чтобы подробно показать процесс решения таких задач. Практически, фиксируется лишь заключительный этап минимизации с представлением на матрице итогового варианта объединения единиц и результата минимизации в аналитической форме.
В примере 2.5.18 получается одно единственное решение задачи. В общем случае минимальных тупиковых форм у функции может быть два и более (пример 2.5.19).
Пример 2.5.19.
Пусть задана функция 

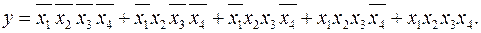
Результаты её минимизации содержат два решения.

При построении объединений рекомендуется их нумеровать, как это делается в приведённых примерах. Площадь матрицы надо выбирать в соответствии со сложностью минимизируемой функции. Повышает различимость представления объединений на матрице в различных цветах. Всё это расширяет предельные возможности метода по размерности функций. Но, предел всё же есть.
С повышением размерности функций и увеличением числа составляющих её минтермов, трудность процедуры минимизации возрастает. Общая картина представления объединений на матрице становится более сложной и запутанной. Возникают трудности чисто визуального характера. Немалые затраты труда требуются при поиске минимальных тупиковых форм функций из-за непомерно возрастающего числа перебираемых вариантов выбора возможных решений. Но, всё же, матричный метод может работать с функциями шести, а может быть, иногда, и семи переменных, что недоступно для метода минимизации с использованием карт Карно.
2.5.5. Минимизация логических функций методом Квайна.
Этот метод, в отличии от двух предыдущих (п. 2.5.3 и п. 2.5.4), носит аналитический характер. Он требует представления исходной функции для минимизации только в СДНФ. Метод реализуется в два этапа.
На первом этапе производится склеивание минтермов минимизируемой функции, то есть, исходных минтермов. Сначала склеиваются минтермы n -ного ранга, где n – размерность минимизируемой функции. Склеивание минтермов производится во всевозможных парных комбинациях. В результате склеивания образуются минтермы (n -1)-ого ранга. Эта процедура может повторяться до (n -1) раз. На каждом шаге склеивания могут оставаться несклеивающиеся минтермы. Их называют первичными импликантами. Логическая сумма всех полученных первичных импликант является тупиковой формой минимизируемой функции. Является ли найденная тупиковая форма искомой минимальной тупиковой формой и, если нет, то какова часть импликантов составит эту форму, станет ясно на втором этапе реализации рассматриваемого метода.
|
|
Дата добавления: 2014-11-09; Просмотров: 1682; Нарушение авторских прав?; Мы поможем в написании вашей работы!