Определенного интеграла

Нахождение площадей плоских фигур с помощью

Решение.

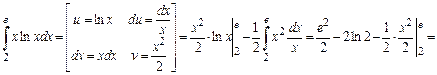
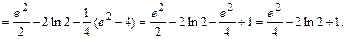
Определенный интеграл 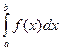от неотрицательной функции численно равен площади криволинейной трапеции, то есть фигуры, ограниченной графиком функции 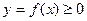, двумя прямыми 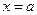, 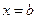и осью .

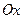В этом состоит геометрический смысл определенного интеграла .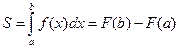

Если 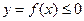, то площадь фигуры, ограниченной графиком этой функции, двумя прямыми 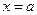, 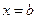и осью 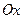, находится по формуле .

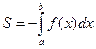Площадь криволинейной фигуры, ограниченной сверху и снизу соответственно линиями 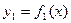, , 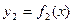слева и справа – прямым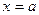и и 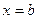, определяется формулой:

.

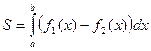Например, вычислить площадь фигуры, ограниченной линиям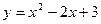и и 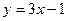. Для построения фигуры найдем точки пересечения этих линий, решим систему:

, .

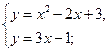
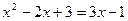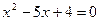Откуда 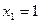, 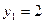и 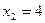, 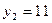. Выполним чертеж фигуры.

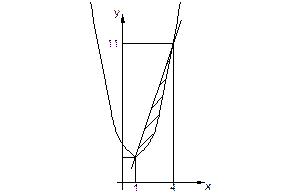
Находим искомую площадь :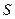

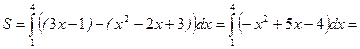
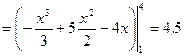(кв. ед. изм.).

Если плоская фигура имеет сложную форму, то ее следует разбить на части так, чтобы можно было применить уже известные формулы.

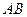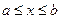С помощью определенного интеграла можно найти длину дуги для кривой с ограничениями по формуле .

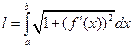Дата добавления: 2014-11-26