
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример. Матрицы и действия над ними
|
|
|
|
Матрицы и действия над ними
Линейная алгебра
Часть I
Математика
П.В. Столбов
Утверждено редакционно-издательским
советом университета в качестве
учебного пособия
Нижний Новгород
ННГАСУ
ББК 22.1
С 81
Столбов П.В. Математика. Часть I [текст]: учебное пособие / П.В. Столбов; Нижегород. гос. архит.-строит. ун-т.– Н.Новгород: ННГАСУ, 2013. – 83 с.
ISBN 978-5-87941-880-2
Учебное пособие и контрольные задания по математике предназначены для студентов заочной формы обучения всех специальностей и направлений.
ББК 22.1
ISBN 978-5-87941-880-2
© Столбов П.В., 2013
© ННГАСУ, 2013
 |
Матрицей порядка  называется прямоугольная таблица чисел, состоящая из
называется прямоугольная таблица чисел, состоящая из  строк и
строк и 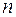 столбцов.
столбцов.
Для обозначения матрицы таблицу чисел заключают в круглые скобки и обозначают заглавными буквами латинского алфавита.
1. 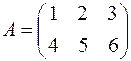 – матрица порядка
– матрица порядка  .
.
2.  – матрица – строка порядка
– матрица – строка порядка  .
.
3.  – матрица – строка порядка
– матрица – строка порядка  .
.
Матрица, в которой число строк совпадает с числом столбцов, называется квадратной.
Пример.  – квадратная матрица порядка
– квадратная матрица порядка 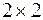 .
.
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы, обозначаются соответствующими строчными буквами латинского алфавита с двумя правыми нижними индексами. Первый индекс обозначает номер строки, а второй – номер столбца, в которых рассматриваемый элемент матрицы находится.
Пример. 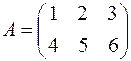 .
.
 –элемент матрицы
–элемент матрицы 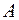 , находящийся во второй строке и в третьем столбце.
, находящийся во второй строке и в третьем столбце.
Заметим, что матрицу 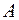 порядка
порядка  можно записать так:
можно записать так:
 ,
, 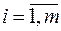 ;
;  .
.
Две матрицы порядка  считаются равными, если все соответствующие элементы этих матриц равны. То есть
считаются равными, если все соответствующие элементы этих матриц равны. То есть  , если
, если  для любых возможных
для любых возможных  и
и  .
.
Пример.  ,
,  . Матрицы
. Матрицы 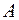 и
и  равны, так как
равны, так как  ,
, 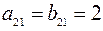 ,
,  .
.
Произведением матрицы 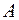 порядка
порядка  на действительное число
на действительное число  называется матрица
называется матрица  того же порядка
того же порядка  , каждый элемент
, каждый элемент  ,
, 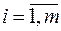 ,
,  которой получен умножением соответствующего элемента
которой получен умножением соответствующего элемента  ,
, 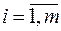 ,
,  исходной матрицы
исходной матрицы 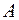 на число
на число  и обозначается:
и обозначается:  .
.
Пример. Найти  , если
, если 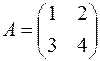 .
.
Решение.  .
.
Ответ:  .
.
Суммой двух матриц  и
и 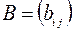 одного порядка
одного порядка  называется матрица
называется матрица  того же порядка
того же порядка  , каждый элемент
, каждый элемент  ,
, 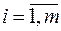 ,
,  которой получен сложением соответствующих элементов
которой получен сложением соответствующих элементов  и
и  ,
, 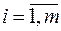 ,
,  и обозначается
и обозначается  .
.
Пример. Найти  , если
, если 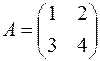 и
и  .
.
Решение.  .
.
Ответ:  .
.
Заметим, что разность двух матриц 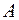 и
и  одного и того же порядка можно определить через сумму и умножение на число
одного и того же порядка можно определить через сумму и умножение на число  , то есть
, то есть  .
.
Пример. Найти  , если
, если 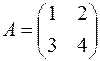 и
и  .
.
Решение. 

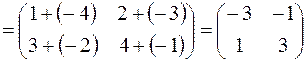 .
.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 798; Нарушение авторских прав?; Мы поможем в написании вашей работы!