
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение ускорений точек тела при плоском движении
|
|
|
|
Лекция 11
Положение точки М по отношению к осям Оху (рис. 11.4) определится радиусом вектора:
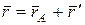 , где
, где 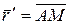 .
.
Дифференцируя дважды уравнение по времени, получим:
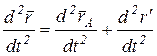 , отсюда следует, что
, отсюда следует, что
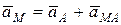 , (11.1)
, (11.1)
где 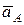 – ускорение точки А (полюс);
– ускорение точки А (полюс);
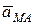 – ускорение точки при вращении вокруг точки А.
– ускорение точки при вращении вокруг точки А.
Так как точка М вращается вокруг полюса А по окружности, то разложим на составляющие – нормальную 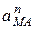 и касательную
и касательную 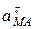 (рис. 11.1):
(рис. 11.1):
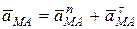
Тогда с учетом (11.1), получим (рис. 11.1а):
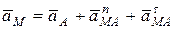 .
.
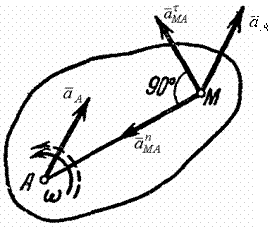
Рис. 11.1
Если полюс А движется не прямолинейно, то его ускорение будет слагаться из касательного и нормального и тогда
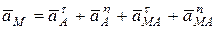 , (11.2)
, (11.2)
Пример 1 (18.11).
Для механизма, представленного на рис. 5.2 угловое ускорение кривошипа ОА 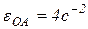 , ОА = 15см. Определить ускорение звена АВ
, ОА = 15см. Определить ускорение звена АВ 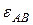 в данном положении механизма, при t = 1c.
в данном положении механизма, при t = 1c.
Решение

Рис. 11.2
Вначале определим ускорение точки В, выбрав за полюс точку А:
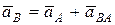 . (1)
. (1)
Так как точка А совершает вращательное движение по окружности вокруг неподвижного центра О, тогда:
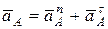 ,
,
где 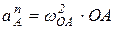 ;
; 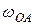 – угловая скорость кривошипа ОА.
– угловая скорость кривошипа ОА.
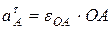 .
.
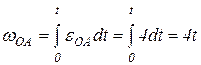 ;
; 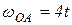 , тогда:
, тогда: 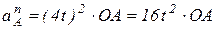 ;
;
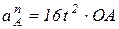 .
.
Точка В совершает вращательное движение вокруг точки А по окружности, тогда
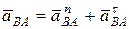 ,
,
где 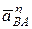 – нормальная составляющая ускорения точки В при вращении вокруг полюса А;
– нормальная составляющая ускорения точки В при вращении вокруг полюса А;
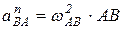 ;
;
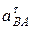 – касательная составляющая ускорения точки В при вращении вокруг полюса А;
– касательная составляющая ускорения точки В при вращении вокруг полюса А;
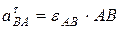 .
.
Для определения 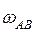 и
и 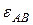 определим скорость в точке В. Построим мгновенный центр скоростей для звена АВ. Точка О является м.ц.с. для звена АВ. Тогда
определим скорость в точке В. Построим мгновенный центр скоростей для звена АВ. Точка О является м.ц.с. для звена АВ. Тогда
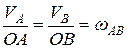 .
.
Так как 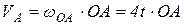 , тогда
, тогда
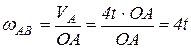 , отсюда
, отсюда 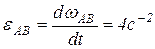 .
.
Изобразим отдельно звено АВ с соответствующими ускорениями (рис. 11.3):
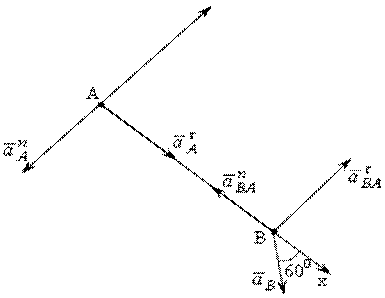
Рис. 11.3
С учетом сделанных расчетов уравнение (1) запишем в виде:
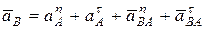 .
.
Спроектируем это векторное уравнение ВА на оси координат:
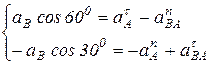 .
.
Подставляя полученные значения, получим:
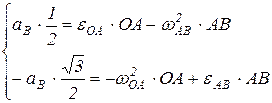 .
.
Из треугольника ОАВ сторона 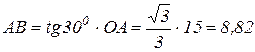 см.
см.
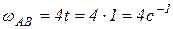 ;
; 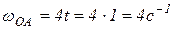 .
.
Тогда 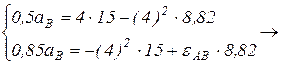
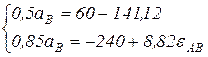
Полученная система двух уравнений имеет две неизвестные: 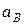 и
и 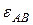 . Решая эту систему относительно неизвестных, получим:
. Решая эту систему относительно неизвестных, получим: 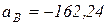 см/с2, знак минус (-) означает, что истинное направление ускорения точки имеет противоположное направление выбранному;
см/с2, знак минус (-) означает, что истинное направление ускорения точки имеет противоположное направление выбранному; 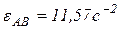 – угловое ускорение звена АВ.
– угловое ускорение звена АВ.
Так как точки D и В принадлежат одному звену DB, которое совершает возвратно-поступательное движение, поэтому все точки этого звена имеют одинаковые скорости и ускорения по величине и направлению. Вследствие этого ускорение точки D будет: 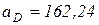 см/с2 и направлено вертикально вверх.
см/с2 и направлено вертикально вверх.
Ответ: 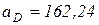 см/с2,
см/с2, 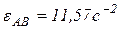 .
.
Пример 2.
На рис. 11.4. представлен механизм в данном положении: 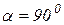 ,
, 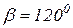 ,
, 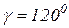 ,
, 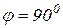 ,
, 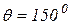 , I1 = 0,6м, I2 = 1,2м, I3 = 1,4м, I4 = 0,8м,
, I1 = 0,6м, I2 = 1,2м, I3 = 1,4м, I4 = 0,8м, 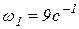 . Определить VA, VB, VD, VE,
. Определить VA, VB, VD, VE, 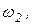
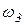 ,
, 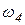 , аА, аВ, аD, аЕ,
, аА, аВ, аD, аЕ, 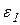 ,
, 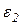 ,
, 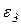 ,
, 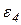 . Точка D является серединой звена I2.
. Точка D является серединой звена I2.

Рис. 11.4
Решение
Определим скорость точки А. Так как точка А движется по окружности, то
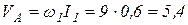 м/с.
м/с.
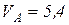 м/с.
м/с.
Вектор скорости 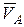 перпендикулярен I1.
перпендикулярен I1.
Вектор скорости точки В направлен перпендикулярно звену I4, а для вычисления модуля, определим мгновенный центр скоростей звена I2, которому принадлежат точки А, В и C2 – является мгновенным центром скоростей звена I2. Составим соотношение:
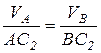 , отсюда
, отсюда 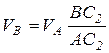 .
.
Так как угол С2ВА = 600, угол ВАС2 = 180-120 = 600, то угол ВС2А = 600.
Это означает, что треугольник ВС2А является равносторонним поэтому
ВС2 =АС2, тогда VB = VA = 5,4 м/с., т.е. VB = 5,4 м/с.
Для определения скорости точки D соединим точку С2 с точкой D и проведем линию, перпендикулярную DC2. Так как в равнобедренном треугольнике медиана является высотой и биссектрисой, то направление вектора скорости точки D совпадет с направлением звена I2. Модуль скорости точки D определим из соотношения:
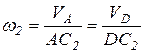 , отсюда
, отсюда 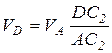 .
.
Из прямоугольного треугольника DC2A следует, что
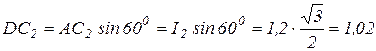 (м)
(м)
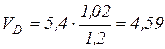 (м/с);
(м/с); 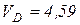 м/с.
м/с.
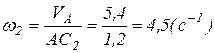 ;
; 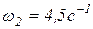 .
.
Направление скорости точки Е совпадает с направляющей ползуна, т.е. имеет вертикальное направление. Зная направления векторов скоростей точек D и Е, принадлежащих звену I3, определим мгновенный центр скоростей звена I3. Это будет точка С3, тогда составим соотношение:
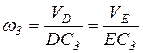 , отсюда
, отсюда 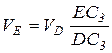 .
.
Рассмотрим треугольник С3DE. Так как угол С3 = 300 и угол Е = 300, то этот треугольник равнобедренный, т.е. DE = DC3;
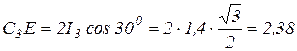 (м);
(м);
Тогда 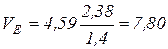 (м/с);
(м/с); 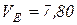 м/с.
м/с.
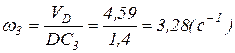 ;
; 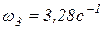 .
.
Определим угловую скорость звена I4:
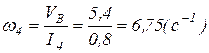 ;
; 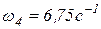 .
.
Определим ускорение точки А (рис. 11.5).

Рис. 11.5
Точка А совершает вращательное движение по окружности вокруг неподвижного центра О1. Поэтому ускорение точки А разложим на нормальную и касательную составляющие:
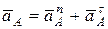 ,
,
где 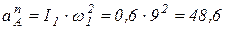 (м/с2);
(м/с2); 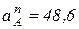 м/с2.
м/с2.
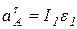 , так как по условию задачи
, так как по условию задачи 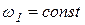 , а
, а 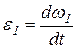 , то
, то 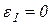 , тогда
, тогда 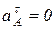 . Поэтому
. Поэтому 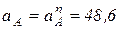 м/с2;
м/с2;  м/с2.
м/с2.
Определим ускорение точки В, выбрав точку А за полюс. Тогда
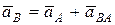 , (1)
, (1)
где 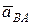 – ускорение, связанное с вращением точки В вокруг А.
– ускорение, связанное с вращением точки В вокруг А.
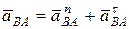 , (2)
, (2)
Подставляя (2) в (1), получим:
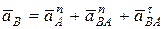 . (3)
. (3)
Так как точка В вращается вокруг неподвижного центра О2, то разложим ускорение точки В на нормальную и касательную составляющие:
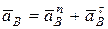 . (4)
. (4)
Подставляя уравнение (4) в уравнение (3), получим:
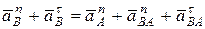 . (5)
. (5)
Выберем оси координат таким образом, что ось х будет направлена вдоль звена I2.
Спроектируем уравнение (5) на оси координат:
| на ось х: |
| на ось у: |
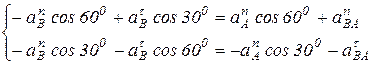 (6)
(6)
Так как: 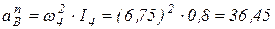 (м/с2);
(м/с2); 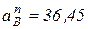 м/с2.
м/с2.
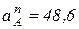 м/с2.
м/с2.
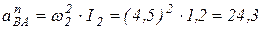 (м/с2);
(м/с2); 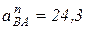 м/с2.
м/с2.
В системе двух уравнений (6) имеется две неизвестные: 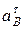 и
и 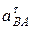 , т.е. система уравнений имеет решение и притом только единственное. Подставим численные значения в систему уравнений (6):
, т.е. система уравнений имеет решение и притом только единственное. Подставим численные значения в систему уравнений (6):
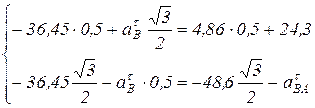
Решая это уравнение, получим:
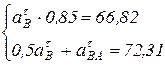 , отсюда следует, что
, отсюда следует, что 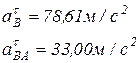
В связи с тем, что 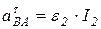 ,
,
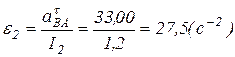 ;
; 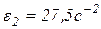 .
.
Ускорение точки В будет:
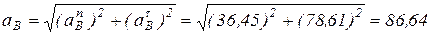 (м/с2);
(м/с2);
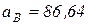 м/с2.
м/с2.
Определим ускорение точки D, выбрав за полюс точку А. Тогда
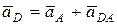 , (7)
, (7)
Так как 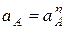 , а ускорение
, а ускорение 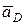 разложим на составляющие
разложим на составляющие 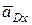 и
и 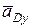 (рис. 11.6).
(рис. 11.6).

Рис. 11.6
Учитывая, что 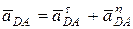 , уравнение (7) примет вид:
, уравнение (7) примет вид:
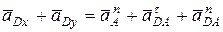 . (8)
. (8)
Спроектируем векторное уравнение (8) на выбранные оси координат:
на ось х: 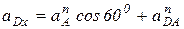
на ось у: 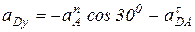 .
.
Полученная система двух уравнений имеет две неизвестные: 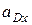 и
и 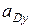 , так как
, так как 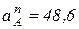 м/с2;
м/с2; 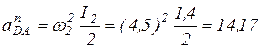 (м/с2);
(м/с2); 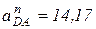 м/с2;
м/с2; 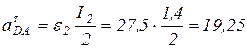 (м/с2);
(м/с2); 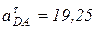 м/с2. Тогда полученная система двух уравнений примет вид:
м/с2. Тогда полученная система двух уравнений примет вид:
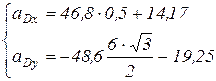
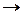
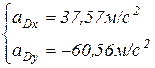
Отрицательное значение 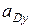 указывает, что истинное направление вектора противоположно выбранному.
указывает, что истинное направление вектора противоположно выбранному.
Ускорение точки D будет:
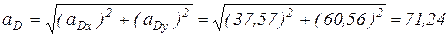 (м/с2);
(м/с2);
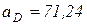 м/с2.
м/с2.
Определим ускорение точки Е. Направление вектора ускорения точки Е, будет совпадать с направляющей ползуна (рис. 11.7). На рис. 11.7 изображен фрагмент механизма, включающий звено I3 и ползун Е.

Рис. 11.7
Ускорение точки Е будем определять, выбрав за полюс точку D, тогда:
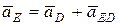 , (9)
, (9)
Учитывая, что 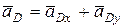 , и
, и 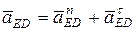 , тогда уравнение (9) примет вид:
, тогда уравнение (9) примет вид:
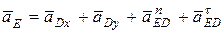 , (10)
, (10)
Выберем оси координат, как показано на рис. 11.7, т.е. ось х направим вдоль направления звена I3 и спроектируем векторное уравнение (10) на оси координат:
на ось х: 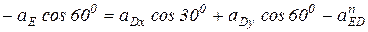
на ось у: 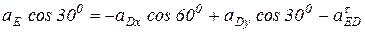 .
.
Представленные два уравнения образуют систему двух уравнений с двумя неизвестными: 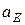 и
и 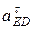 , так как
, так как 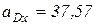 м/с2;
м/с2; 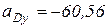 м/с2;
м/с2; 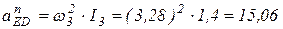 (м/с2), т.е.
(м/с2), т.е. 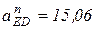 м/с2. Подставляя численные значения, получим систему двух уравнений с двумя неизвестными:
м/с2. Подставляя численные значения, получим систему двух уравнений с двумя неизвестными:
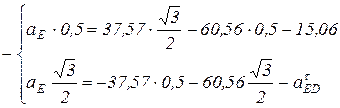
После преобразований получим:
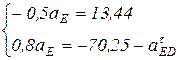 отсюда следует
отсюда следует 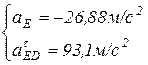
Ускорение точки Е составляет 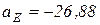 м/с2 (знак минус указывает, что истинное направление вектора ускорения имеет противоположное значение выбранному).
м/с2 (знак минус указывает, что истинное направление вектора ускорения имеет противоположное значение выбранному).
Так как 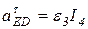 , то
, то 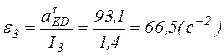 , т.е.
, т.е. 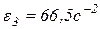 .
.
Таким образом, определены все значения кинематических характеристик, указанные в вопросе задачи.
Вопросы для самоконтроля
1. Определение ускорений точек твердого тела?
2. Определение углового ускорения твердого тела при плоском движении?
Задачи, рекомендуемые для самостоятельного решения: 18.1 – 18.36 [2].
Литература: [1], [3], [4].
 Лекция 12
Лекция 12
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 1301; Нарушение авторских прав?; Мы поможем в написании вашей работы!