Сложение ускорений

Сложение скоростей

Теорема. При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей:

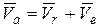, (12.1)

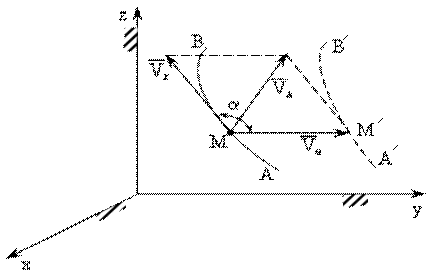
Рис. 12.2

На рис. 12.2: АВ – траектория точки М в относительном движении;

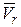– относительная скорость точки М;

А₁В₁– положение траектории точки М вследствие переносного движения.

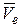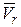Если угол между и составляет α, то формула (12.1) в скалярном виде будет:

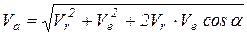, (12.2)

Теорема Кориолиса. Абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного, характеризующего изменение относительной скорости в относительном движении; переносного, характеризующего изменение скорости в переносном движении и кориолисово, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости в относительном движении.

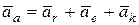, (12.3)

где 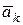– кориолисово ускорение.

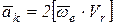. (12.4)

Кориолисово ускорение точки равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки. Если угол между векторами и 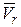составляет угол α, то модуль кориолисова ускорения будет равен:

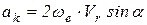. (12.5)

Частные случаи. Кориолисово ускорение будет равно нулю в следующих случаях:

1. Когда 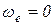, т.е. переносное движение является поступательным, или, если угловая скорость равна нулю;

2. Когда 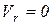, т.е. когда относительная скорость равна нулю;

3. Когда 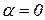и 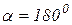, т.е. когда относительное движение происходит по направлению, параллельному оси переносного вращения или, если в данный момент времени вектор 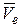параллелен этой оси.

Определение направления кориолисова ускорения (правило Жуковского Е.Н.):

Для определения направления кориолисова ускорения необходимо выполнить следующее:

5. провести плоскость, перпендикулярную вектору угловой скорости;

6. спроектировать на эту плоскость вектор скорости в относительном движении;

7. повернуть проекцию вектора скорости на 90⁰ по ходу вращения переносного движения.

Пример 1.

Точка М в относительном движении из положения 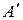движется по диагонали квадрата BCDA по закону 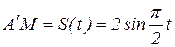, см. Квадрат BCDA вращается вокруг неподвижной оси по закону 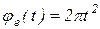, рад. Сторона квадрата CD = 4см. Определить абсолютную скорость и абсолютное ускорение при t = 1c.

Решение

Рис. 12.3

Определим абсолютную скорость точки М в момент времени t = 1c. Точка М перемещается по диагонали прямоугольника из положения 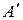. Так как относительное движение прямолинейное, то скорость точки М в относительном движении будет:

.

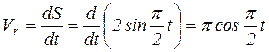При t = 1c 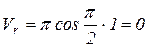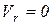(м/с); м/с.

Вращательное движение точки М вокруг оси ОО₁ является переносным движением. Траектория переносного движения является окружность с радиусом r. Определим положение точки М на прямой АВ при t = 1c.

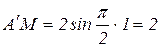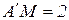(см); см.

Из треугольника MDK следует, что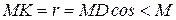

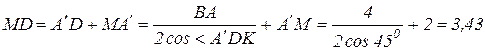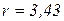(см);

см.

Так как точка М совершает в переносном движении вращение по окружности с радиусом r, то скорость в переносном движении будет:

,

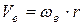где 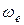– угловая скорость переносного движения.

;

.

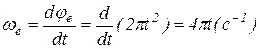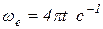Тогда

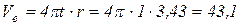(см/с);

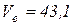см/с.

Вектор скорости направлен по касательной к траектории в точке М, т.е. перпендикулярно плоскости чертежа.

Так как при сложном движении точки:

,

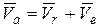то вследствие того, что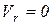

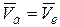, тогда 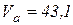см/с.

Абсолютная скорость точки М при t = 1c по модулю равна 43,1 см/с и направлена перпендикулярно плоскости чертежа (на нас).

Определим абсолютное ускорение точки М согласно теоремы сложения ускорений:

.

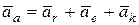Так как в относительном движении точка движется по прямой, то:

.

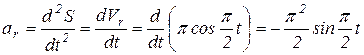При t = 1c, 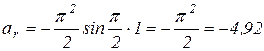(см/с²);

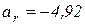см/с².

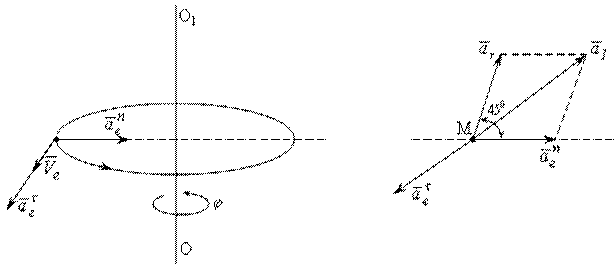
Вследствие движения точки М в переносном движении по окружности (рис. 12.4а):

,

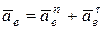где 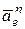– нормальная составляющая ускорения в переносном движении.

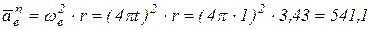(см/с²);

см/с²., вектор нормальной составляющей ускорения направлен по радиусу к оси вращения.

;

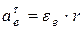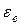– угловое ускорение в переносном движении;

; .

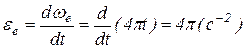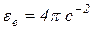Тогда ; .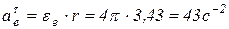

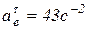Вектор касательной составляющей ускорения направлен в сторону направления вектора скорости (так как движение ускоренное, вследствие того, что ), т.е. перпендикулярно плоскости чертежа (на нас).

а) б)

Рис. 12.4

Определим кориолисово ускорение:

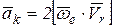
или в скалярной форме:

,

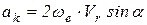где 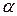– угол между векторами и .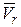

Так как 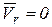, то и кориолисово ускорение равно нулю, т.е.:

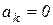см/с².

В результате проведенных вычислений установлено, что на точку М в момент времени t = 1c действует три составляющих ускорения: 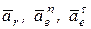(рис. 12.4б). Векторы 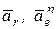лежат в плоскости чертежа и угол между ними составляет 45⁰, тогда модуль суммы этих двух векторов будет:

,

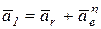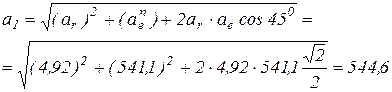(см/с²);

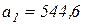см/с².

Вектор 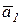находится в плоскости чертежа, а вектор 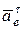– перпендикулярен плоскости чертежа, тогда результирующий вектор – вектор абсолютного ускорения будет:

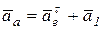
или в скалярной форме:

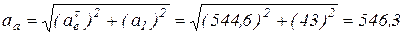(см/с²);

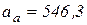см/с².

Ответ: 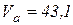см/с, 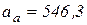см/с².

Пример 2.

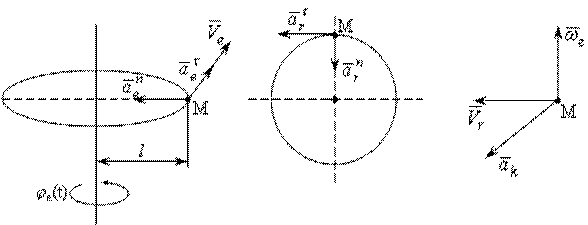
Точка М перемещается по окружности диска радиусом R = 2 см по закону 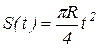из положения А. Диск вращается вокруг неподвижной оси по закону 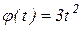. Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1c.

Решение

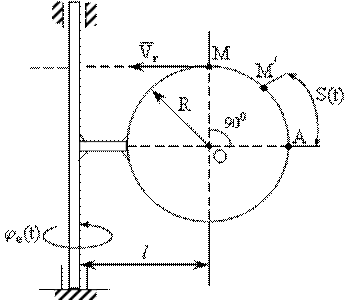
Рис. 12.5

R = 2см;

l = 5см.

Анализ характера движения точки М (рис. 12.5) свидетельствует, что движение по окружности диска радиусом R является относительным, а движение диска вокруг неподвижной оси – переносное движение.

Определим положение точки М на окружности диска в момент t = 1c:

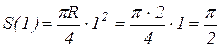(см).

Длина дуги, пройденная точкой М за 1с, составляет 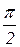см. Определим длину дуги в радианах:

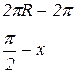
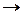
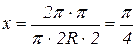(рад.)

Отсюда следует, что дуга, пройденная точкой М за 1с, составляет 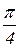рад., или 90⁰ (положение М). Направление вектора скорости 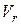будет направлено по касательной к окружности в этой точке (рис. 12.5).

Определим абсолютную скорость точки М в момент t = 1c. По правилу сложения скоростей:

.

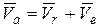Модуль скорости в относительном движении будет:

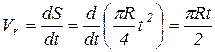; при t = 1c.

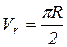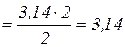(см/с) см/с.

В переносном движении точка М совершает вращательное движение по окружности с радиусом вокруг неподвижной оси (рис. 12.6а).

а) б) в)

Рис. 12.6

Направление вектора переносной скорости 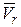перпендикулярно плоскости чертежа в сторону «от нас».

Модуль скорости 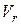определим:

,

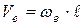где 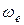– угловая скорость вращения диска вокруг оси.

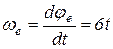; при t = 1c .

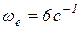Тогда

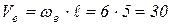(см/с);

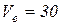см/с.

Векторы скоросте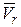й и 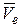ортогональны, так как расположены в двух взаимно пересекающихся плоскостях. Поэтому модуль результирующего вектора 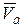определим:

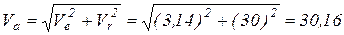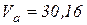(см/с);

см/с.

Определим абсолютное ускорение точки М в момент времени t = 1c. Согласно правилу сложения ускорений:

.

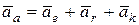В относительном движении ускорение точки М разложим на две составляющие 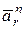и 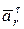, так точка движется по окружности (рис. 12.6б):

,

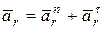где 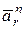– нормальная составляющая вектора ускорения точки М в относительном движении.

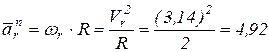(см/с); 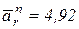см/с.

Вектор 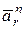направлен по радиусу к центру окружности О.

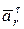– касательная составляющая вектора ускорения точки М в переносном движении.

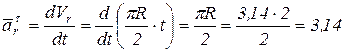(см/с²); 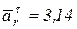см/с².

Вектор 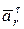направлен по касательной и окружности и совпадает с направлением вектора скорости, так как движение ускоренное.

Так как в переносном движении точка М движется по окружности вокруг неподвижной оси, то ускорение разложим на составляющие (рис. 12.6а):

,

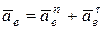где 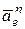– нормальная составляющая вектора ускорения в переносном движении.

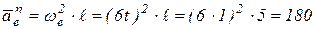(см/с²); 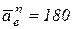см/с².

Вектор 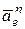направлен к неподвижной оси.

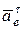– касательная составляющая вектора ускорения в переносном движении.

;

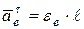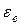– угловое ускорение диска в переносном движении:

; .

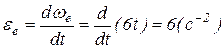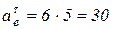(см/с²); 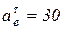см/с².

Вектор 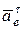направлен перпендикулярно плоскости чертежа и совпадает с направлением вектора скорости переносного движения (так как движение ускоренное).

Определим кориолисово ускорение:

.

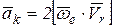Модуль кориолисова ускорения равен:

,

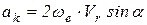где 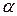– угол между векторами и .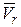

Согласно «правила буравчика» в данном случае вектор угловой скорости переносного движения направлен параллельно неподвижной оси, вокруг которой вращается диск. Тогда расположение векторов и 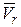будет таким, как представлено на рис. 12.6в. В этом случае вектор кориолисова ускорения, согласно правила Жуковского, будет направлен перпендикулярно плоскости чертежа «на нас».

Модуль 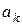будет равен:

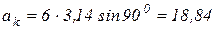(см/с²);

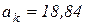см/с².

Таким образом, на точку М действуют пять составляющих ускорений (рис. 12.7).

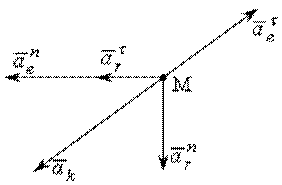
Рис. 12.7

Векторы 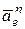и 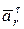лежат вдоль одной прямой в одну сторону, поэтому сумма этих векторов будет:

,

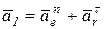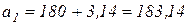(см/с²).

Векторы 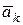и 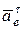направлены вдоль одной прямой, но в противоположные стороны, тогда результирующий вектор 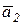будет:

,

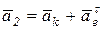(см/с²).

Получившаяся система векторов 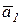, 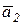и 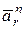образуют ортогональную систему, т.е. взаимноперпендикулярны, поэтому результирующий вектор 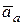можно представить:

,

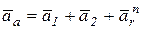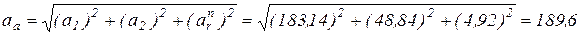(см/с²)

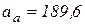см/с².

Ответ: 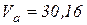см/с, 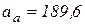см/с².

Вопросы для самоконтроля

1. Что такое сложное движение точки?

2. Что такое относительное движение? Его кинематические характеристики?

3. Что такое переносное движение? Его кинематические характеристики?

4. Что такое абсолютное движение? Его кинематические характеристики?

5. Как определяется абсолютная скорость точки?

6. Теорема Кориолиса?

7. Как определяется величина и направление кориолисова ускорения?

Задачи, рекомендуемые для самостоятельного решения: 22.1 – 22.24, 23.1 – 23.66 [2].

Литература: [1], [3], [4].

Приложения

Приложение 1

Программа по теоретической механике (извлечение)

Дата добавления: 2014-11-26