Определение: Числа и называются комплексно – сопряженными

Лекция № 9 Комплексные числа.

Цель: Рассказать о введении комплексного числа, о расширении поля действительных чисел до поля комплексных чисел. Научить выполнять действия над комплексными числами, переводить комплексные числа из одной формы в другую.

1. Комплексные числа. Геометрическое изображение комплексных чисел.
2. Действия над комплексными числами.
3. Формы комплексных чисел.

1. Комплексные числа.

Определение: Комплексным числом z называется выражение 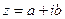, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

При этом число a называется действительной частью числа z (a = Re z), а b - мнимой частью (b = Im z).

Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.

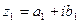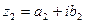Определение: Два комплексных числа и называются равными, если соответственно равны их действительные и мнимые части:

Определение: Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части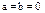

Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.

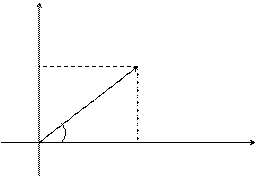Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.

у

A(a, b)

r b

j

0 a x

Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.

С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.

2. Действия с комплексными числами.

Основные действия с комплексными числами вытекают из действий с многочленами.

1) Сложение и вычитание.

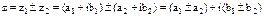
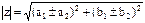
2) Умножение.

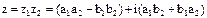
В тригонометрической форме:

,

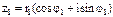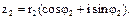
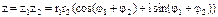
С случае комплексно – сопряженных чисел:

3) Деление.

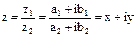
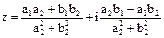
В тригонометрической форме:

4) Возведение в степень.

Из операции умножения комплексных чисел следует, что

В общем случае получим: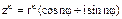

где n – целое положительное число.

Это выражение называется формулой Муавра.

(Абрахам де Муавр (1667 – 1754) – английский математик)

Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.

5) Извлечение корня из комплексного числа.

Возводя в степень, получим: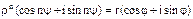

Отсюда: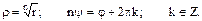

Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.

3. Тригонометрическая форма числа.

Из геометрических соображений видно, что 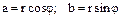. Тогда комплексное число можно представить в виде:

Такая форма записи называется тригонометрической формой записи комплексного числа.

При этом величина r называется модулем комплексного числа, а угол наклона j - аргументом комплексного числа. .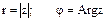

Из геометрических соображений видно:

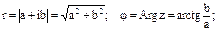
Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.

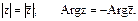
Показательная форма комплексного числа.

Рассмотрим показательную функцию

Можно показать, что функция w может быть записана в виде:

Данное равенство называется уравнением Эйлера. Вывод этого уравнения будет рассмотрен позднее. (См.).

Для комплексных чисел будут справедливы следующие свойства:

1)

2)

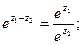
3) где m – целое число.

Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем: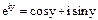

Для комплексно – сопряженного числа получаем: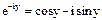

Из этих двух уравнений получаем: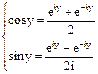

Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.

Если представить комплексное число в тригонометрической форме: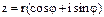

и воспользуемся формулой Эйлера: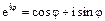

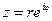
Полученное равенство и есть показательная форма комплексного числа.

Дата добавления: 2014-11-26