Лекция № 11 Пределы

Лекция № 10 Функция.

Цель: Ввести понятие функции, переменной величины (зависимой, независимой). Рассмотреть основные виды функций, свойства функций.

1. Определение функции. Способы задания функции.
2. Виды функций.
3. Свойства функций.

1. Определение: Функция – это правило или закон, по которому одной переменной величине х (независимой) сопоставляется другая переменная величина у (зависимая).

Обозначается как у = f(x).

Определение: Множество всех значений х, для которых функция существует, называется областью определения функции. D(x).

Определение: Множество всех значений у, для которых функция существует, называется областью значения функции. Обозначается как E(y).

Способы задания функции:

· Аналитический способ, если функция задана формулой вида у = f (х). Аналитическое задание состоит в том, что дается формула указывающая, какие математические действия следует выполнить над каждым значением аргумента функции. Этот способ наиболее часто встречается на практике.

· Табличный способ состоит в том, что функциональная зависимость задается в виде таблицы, содержащей ряд числовых значений аргумента и соответствующих им значений функции. Этот способ является наиболее удобным, когда изучается зависимость между переменными величинами по результатам наблюдения.

· Графический способ задания функции состоит в том, что в данной прямоугольной системе координат задается некоторая кривая. Абсцисса каждой точки кривой дает значение аргумента х, а ордината той же точки – соответствующее значение формуле у.

· Словесный способ, если функция описывается правилом ее составления.

2. Функции бывают алгебраические и трансцендентные (сложные).

С алгебраическими функциями встречались в школьном курсе алгебры.

· Степенная функция у = х ⁿ, где n – действительное число.

· Показательная функция у = а ^х, где а – положительное число, не равное единице.

· Логарифмическая функция y = log _a x, где основание логарифма а – положительное число, не равное единице.

· Тригонометрические функции: y = sin x, y = cos x, y = tg x, y = ctg x.

· Обратные тригонометрические функции: y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.

Сложные функции представляют собой зависимость одной функции от другой.

3. Свойства функций.

· Четность, нечетность. f (-х) = f (х) – четная, f (-х) = -f (х) – нечетная.

· Монотонность. Возрастание и убывание функции.

· Ограниченность.

· Периодичность.

Цель: Ввести понятия предела последовательности, предела функции, бесконечно большой и бесконечно малой величин. Рассмотреть основные теоремы о пределах, замечательные пределы. Закрепить эти понятия на практике.

1. Предел последовательности. Предел функции.
2. Основные теоремы о пределах.
3. Замечательные пределы.

1. Предел функции в точке.

y f(x)

A + e

A

A - e

0 a - D a a + D x

Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)

Определение: Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что 0 < ïx - aï < D верно неравенство ïf(x) - Aï< e.

То же определение может быть записано в другом виде: Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.

Запись предела функции в точке: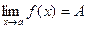

Определение: Если f(x) ® A₁ при х ® а только при x < a, то - называется пределом функции f(x) в точке х = а слева, а если f(x) ® A₂ при х ® а только при x > a, то 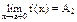называется пределом функции f(x) в точке х = а справа.

у

f(x)

А₂

А₁

0 a x

Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы А₁ и А₂ называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).

Предел функции при стремлении аргумента к бесконечности.

Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство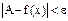

При этом предполагается, что функция f(x) определена в окрестности бесконечности.

Записывают: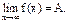

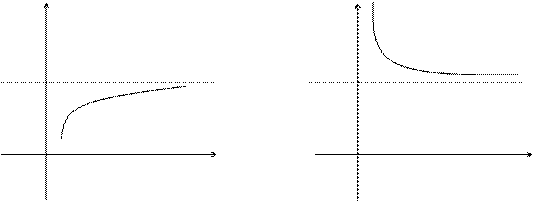Графически можно представить:

y y

A A

0 0

x x

y y

A A

0 0

x x

Аналогично можно определить пределы 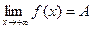для любого х>M и

для любого х<M.

2. Основные теоремы о пределах.

Теорема 1: , где С = const.

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.

Теорема 2:

Теорема 3:

Следствие:

Теорема 4: 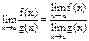при

Теорема 5: Если f(x)>0 вблизи точки х = а и 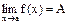, то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

Теорема 6: Если g(x) £ f(x) £ u(x) вблизи точки х = а и 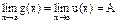, то и .

Бесконечно малые функции.

Определение: Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если .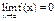

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Свойства бесконечно малых функций:

1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Определение. Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенствоïf(x)ï>M выполняется при всех х, удовлетворяющих условию 0 < ïx - aï < D

Записывается .

Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим: а если заменить на f(x)<M, то:

Графически приведенные выше случаи можно проиллюстрировать следующим образом:

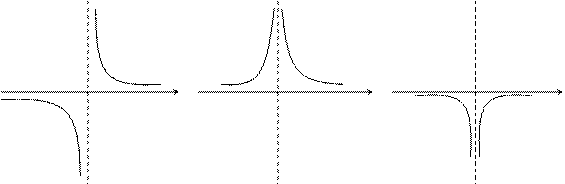a x a x a x

Определение. Функция называется бесконечно большой при х®а, где а – число или одна из величин ¥, +¥ или -¥, если 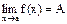, где А – число или одна из величин ¥, +¥ или -¥.

Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.

3. Некоторые замечательные пределы.

Первый замечательный предел. 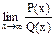, где P(x) = a₀xⁿ + a₁x^n-1 +…+a_n,

Q(x) = b₀x^m + b₁x_m-1 +…+b_m - многочлены.

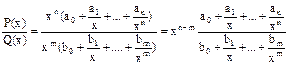
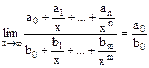
Итого:

Второй замечательный предел.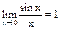

Третий замечательный предел.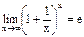

Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.

Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения: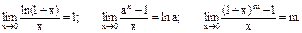

Дата добавления: 2014-11-26