Лекция № 5 Декартова система координат в пространстве

М

r₁

r₂

F₁ O F₂ х

F₁, F₂ – фокусы. F₁ = (c; 0); F₂(-c; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема: Фокусное расстояние и полуоси эллипса связаны соотношением: a² = b² + c².

Определение: Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Е = с/a. Т.к. с < a, то е < 1.

Определение: Величина k = b/a называется коэффициентом сжатия эллипса, а величина

1 – k = (a – b)/a называется сжатием эллипса.

Коэффициент сжатия и эксцентриситет связаны соотношением: k² = 1 – e².

Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

Если для точки М(х₁, у₁) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне эллипса.

С эллипсом связаны две прямые, называемые директрисами.

Их уравнения: x = a/e; x = -a/e.

3. Гипербола.

F₂

F₁

b

r₂

r₁

M(x, y)

Определение: Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

По определению ïr₁ – r₂ï= 2a. F₁, F₂ – фокусы гиперболы. F₁F₂ = 2c.

каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых

Определение: Отношение называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

Определение: Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются

4. Парабола.

Определение: Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Расположим начало координат посередине между фокусом и директрисой.

у

А М(х, у)

Величина р (расстояние от фокуса до директрисы) называется параметром параболы. Каноническое уравнение параболы y² = 2px.

Уравнение директрисы: x = -p/2.

Цель: Ввести понятие свободного вектора, разложение вектора в базисе по единичным векторам. Определить действия над векторами как геометрически, так и алгебраически. Рассмотреть три произведения векторов и их геометрический смысл.

1. Понятие вектора на плоскости и в пространстве.
2. Скалярное произведение векторов.
3. Векторное произведение векторов.
4. Смешанное произведение векторов.

1. Пусть О_х, О_у, О_z – три взаимно перпендикулярные оси в трехмерном пространстве (оси координат), исходящие из общей точки О (начало координат).

Три взаимно перпендикулярные плоскости О_уz, О_ху, О_хz, проходящие через соответствующие оси, называются координатными плоскостями.

Z О_хуz – прямоугольная система

М₃ координат в пространстве

О_х – ось абсцисс

О_у – ось ординат

М О_z – ось аппликат

О i, j, k – единичные векторы

k a (орты) на осях О_х, О_у, О_z

Для каждой точки М

i j У

пространства $ ее радиус

N вектор а = ОМ, начало которого

Х есть данная точка М.

Определение: Под декартовыми прямоугольными координатами х, у, z точки М понимаются проекции ее радиуса-вектора а на соответствующие оси координат, т.е. х = а_х, у = а_у, z = а_z

Проведем через вектора, плоскости параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями М₁, М₂, М₃, тогда на этих осях получатся направленные отрезки ОМ₁ = х, ОМ₂ = у, ОМ₃ = z, численно равные координатам точки М.

А = ахi + ауj +аzk	- разложение вектора по ортам координатных осей
	ах, ау, аz – координаты вектора а; а (ах, ау, аz)

Операции над векторами:

1. сумма векторов

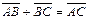
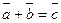
а) правило треугольника:

В

а

в

А с

С

б) правило параллелограмма:

А в С

а +в

а

О В

в

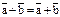
Свойства сложения векторов:

1) (коммутативность)

2) (ассоциативность)

2. разность векторов

Для любых векторов и сумма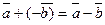

А

в а -в

а

О а-в В

3. произведение вектора на число

Произведение вектора на число называется вектор, длина которого равна , а направление совпадает с направлением вектора , если 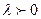, и противоположно ему, если

4. Модуль вектора.

Длину вектора можно вычислить по аналогии с длиной отрезка по формуле:

|а| = Öах^2 + ау^2 + аz^2

- модуль (длина) вектора а

2. Скалярное произведение векторов.

Определение. Скалярным произведением векторов и называется число, равное произведению их длин на косинус угла между ними.

× = ï ïï ïcosj

Свойства скалярного произведения:

1) × = ï ï²;

2) × = 0, если ^ или = 0 или = 0.

3) × = × ;

4) ×( + ) = × + × ;

5) (m )× = ×(m ) = m( × );

3. Векторное произведение векторов.

Определение. Векторным произведением векторов и называется вектор 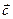, удовлетворяющий следующим условиям:

1) , где j - угол между векторами и ,

2) вектор 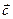ортогонален векторам и

3) , и 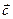образуют правую тройку векторов.

Обозначается: или .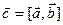

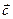
j

Свойства векторного произведения векторов:

1) ;

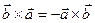2) , если ïï или = 0 или = 0;

3) (m )´ = ´(m ) = m( ´ );

4) ´( + ) = ´ + ´ ;

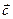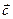5) Если заданы векторы (x_a, y_a, z_a) и (x_b, y_b, z_b) в декартовой прямоугольной системе координат с единичными векторами , то

´ =

6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .

4. Смешанное произведение векторов.

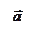
Определение. Смешанным произведением векторов , и 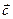называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов и .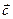

Обозначается или (, , ).

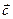Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , и .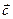

Свойствасмешанного произведения:

1)Смешанное произведение равно нулю, если:

а)хоть один из векторов равен нулю;

б)два из векторов коллинеарны;

в)векторы компланарны.

2)

3)

4)

5) Объем треугольной пирамиды, образованной векторами , и 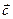, равен

6)Если , , то

Дата добавления: 2014-11-26