Лекция №1 Системы координат

Цель: Ввести понятие систем координат. Рассмотреть два вида систем: декартовую прямоугольную и полярную системы координат. Научить переводить координаты точек из одной системы в другую при помощи формул связи между системами. Ввести формулы расстояния между двумя точками и деления отрезка в данном отношении и закрепить их на практике.

1. Понятие системы координат.
2. Прямоугольная система координат.
3. Полярная система координат. Связь между прямоугольной и полярной системами координат.
4. Простейшие задачи: расстояние между точками, деление отрезка в данном отношении.

1. Для определения положения произвольной точки могут использоваться различные системы координат. Положение произвольной точки в какой-либо системе координат должно однозначно определяться. Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса. Как на плоскости, так и в пространстве возможно задание самых разнообразных систем координат. Выбор системы координат зависит от характера поставленной геометрической, физической или технической задачи. Рассмотрим некоторые наиболее часто применяемые на практике системы координат.

2. Зафиксируем в пространстве точку О, и рассмотрим произвольную точку М. Положение точки в пространстве будет определяться координатами на осях ОХ, ОУ, OZ. Координаты точки – это расстояния от начала координат до проекций точки М на оси.

Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.

1-я ось – ось абсцисс

2-я ось – ось ординат

3-я ось – ось аппликат

3. Определение. Точка О называется полюсом, а луч l – полярной осью.

Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.

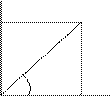М

r

r =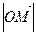

j

0 1

Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.

Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями: x = rcosj; y = rsinj; x² + y² = r²

4. Пусть даны точки А(х₁, у₁, z₁) и В(х₂, у₂, z₂).

Расстояние между ними находится по формуле .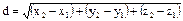

Координаты точки М, делящей отрезок АВ в отношении l, находятся по формулам:

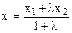
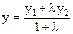
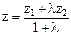
Дата добавления: 2014-11-26