Транспортирование матрицы

Умножение двух матриц

Сложение и умножение матриц, вычитание

Определители

Комплексные числа

Дифференциальные уравнения первого порядка

Корни характеристического уравнения:

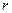
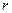
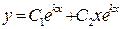
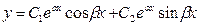
Пример.

1. Решить дифференциальное уравнение .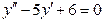

Решение: .

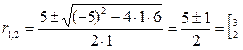
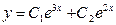
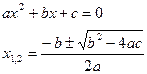
2. Решить дифференциальное уравнение .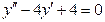

3. Решить дифференциальное уравнение .

1. Вычислить .

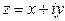– алгебраическая форма

Пример.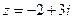

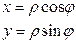
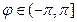
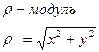
– тригонометрическая форма.

2. Найти , если ,

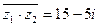
Ответ: .

,

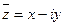
3. Найти i

Ответ: -1.

4. Найти , ,

Ответ: .

5. Найти , ,

Ответ: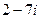

1. Решить систему уравнений по формулам Крамера:

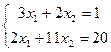
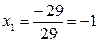
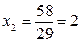
Ответ: (-1;2).

Проверка:

2. Найти обратную матрицу:

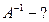
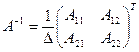
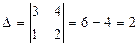
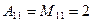
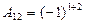
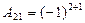
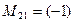
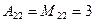
3. Найти , где ,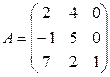

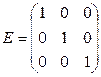
Ответ: .

1.

2.

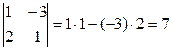
3.

4.

5.

6. Найти М₁₂:

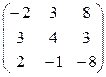
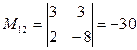
6. Найти А₂₁ и А₃₃

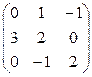
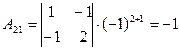
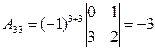
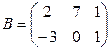
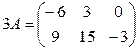
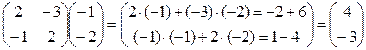Ответ: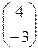

2х2 2х1 2х1 2х1

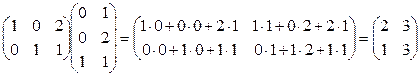
2х3 3х2 2х2 2х2

i -строка, j -столбец

Разложение по первой строке

Разложение по первому столбцу

Правило треугольников (Саррюса)

-

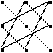
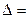
М₁₃ вычеркиваем первую строку и третий столбец

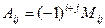
1. Складывать и вычитать можно только матрицы с одинаковым количеством строк и столбцов.

2. При умножении двух матриц количество столбцов первой матрицы должно равняться количеству строк второй матрицы. Иначе нельзя:

Единичная матрица 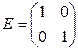II порядка 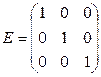III порядка

Ранг матрицы – максимальный порядок миноров, отличных от нуля.

В ступенчатой матрице ранг равен числу ненулевых строк.

Обратная матрица:

Транспонированная матрица:

Записать первую строку как первый столбец, вторую строку как второй столбец и т.д.

Формулы Крамера:

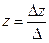
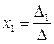
в определителе вместо первого столбца ставили столбец свободного членов;

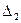вместо второго столбца;

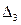вместо второго столбца.

1. Найти угловой коэффициент прямой .

Ответ: 3, так как , где k – угловой коэффициент.

2. Найти угловой коэффициент прямой, параллельной прямой . . 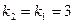Ответ: 3.

3. Найти угловой коэффициент прямой, перпендикулярной прямой . . Ответ: .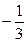

4. Найти угловой коэффициент прямой .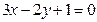

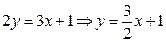. Ответ: .

5. Найти коэффициент прямой, параллельной прямой .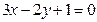

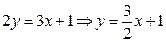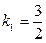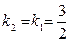, , . Ответ: .

6. Найти угловой коэффициент прямой, перпендикулярной прямой .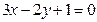

, , .

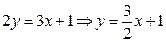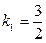7. Найти уравнение прямой, проходящей через точку (-1;2) параллельно прямой .

Решение: .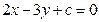

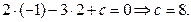Ответ: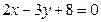

8. Найти уравнение прямой, проходящей через точку (1;3) перпендикулярно прямой .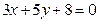

Решение: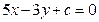

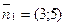, , берем . .

Найдем с: с=4. Ответ: .

Уравнение прямой с угловым коэффициентом , где – угловой коэффициент.

Условие параллельности // Условие перпендикулярности

//

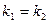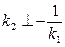
Общее уравнение прямой на плоскости:

, где -нормаль.

Условие параллельности прямых:

.

Условие перпендикулярности прямых:

.

Уравнение прямой, проходящей через точки:

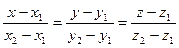
Каноническое уравнение прямой:

, где (m, n, p) – направляющей вектор.

Уравнение окружности:

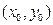– центр, – радиус.

1. Найти радиус окружности

. Ответ: 3.

2. Составить уравнение окружности с центром в точке С(1;1) и радиусом R=4. Ответ: .

1. Найти уравнение прямой, проходящей через точку А(1;0), В(2;1).

.

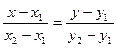
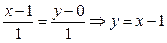2. Найти координаты точки пересечения прямых 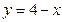и . Ответ: .

3. Найти нормальный вектор прямой 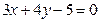. Ответ: (3;4).

4. Найти направляющий вектор прямой 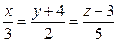. Ответ: (3;2;5).

5. Вычислить площадь треугольника, отсекаемого прямой 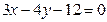от координатного угла.

.

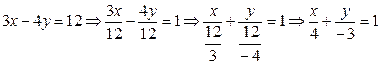
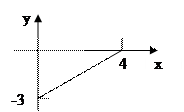
6. Найти уравнение прямой, проходящей через точки А(-1;3) и В(2;5).

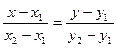
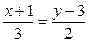
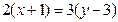, , . Ответ: .

1. Найти область определения функции .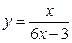

. Ответ: .

2. Найти область определения функции .

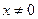
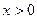
Ответ: .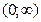

3. Найти область определения функции 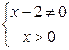. Ответ: .

4. Найти область определения функции . . Ответ: .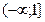

5. Найти максимум функции .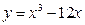

.

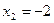
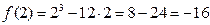Ответ: максимум=-16.

6. Найти интервалы убывания функции

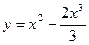
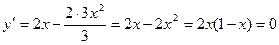
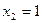
Ответ: .

7. Найти минимум функции

.

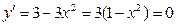
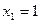
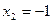
Ответ: -4.

Дата добавления: 2014-11-09