
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сложение векторов. Умножение векторов на числа
|
|
|
|
В множестве V (E3) векторов пространства определим операции сложения векторов и умножения векторов на вещественные числа.
Пусть 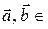 V (E3). Отложим вектор
V (E3). Отложим вектор 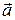 от некоторой точки
от некоторой точки  т.е. построим точку
т.е. построим точку 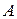 такую, что
такую, что 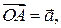 затем от точки
затем от точки 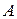 отложим вектор
отложим вектор  т.е. построим точку
т.е. построим точку 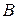 такую, что
такую, что 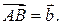 Рассмотрим вектор
Рассмотрим вектор  (рис. 10).
(рис. 10).
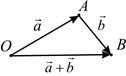
Рис. 10
Покажем, что полученный вектор будет одним и тем же независимо от выбора точки 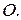 Другими словами, пусть
Другими словами, пусть 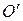 – точка, отличная от точки
– точка, отличная от точки 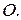 Повторим операции откладывания этих же векторов, но от точки
Повторим операции откладывания этих же векторов, но от точки 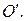 Получим точки
Получим точки 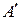 и
и 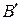 такие, что
такие, что 
 Убедимся, что
Убедимся, что 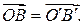
Утверждение 1.2.1. Пусть  E3,
E3, 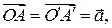
 Тогда
Тогда 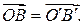
Доказательство. По условию,  поэтому по следствию 1.1.1 утверждения 1.1.1 имеем:
поэтому по следствию 1.1.1 утверждения 1.1.1 имеем: 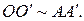 Аналогично, из условия
Аналогично, из условия  получаем, что
получаем, что 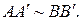 Следовательно,
Следовательно, 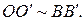 Еще раз применяя следствие 1.1.1, получаем
Еще раз применяя следствие 1.1.1, получаем 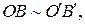 что и означает искомое равенство
что и означает искомое равенство 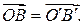
Доказанное утверждение делает корректным следующее определение.
Определение 1.2.1. Суммой вектора  и вектора
и вектора  называется вектор
называется вектор 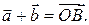
Таким образом, для любых трех точек 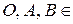 E3 верно равенство
E3 верно равенство
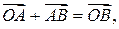 (2)
(2)
которое называется равенством треугольника.
Упражнение 1,2.1. Докажите, что сумма двух неколлинеарных векторов  и
и  может быть вычислена по следующему правилу параллелограмма: сумма векторов-сторон параллелограмма равна вектору-диагонали
может быть вычислена по следующему правилу параллелограмма: сумма векторов-сторон параллелограмма равна вектору-диагонали 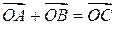 (рис. 11).
(рис. 11).
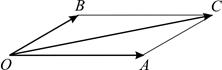
Рис. 11
Отметим следующие основные свойства сложения векторов, справедливые для любых векторов 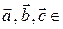 V (E3).
V (E3).
Теорема 1.2.1. (i) 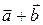 =
= 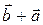 (коммутативность сложения векторов);
(коммутативность сложения векторов);
(ii) 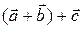 =
=  (ассоциативность сложениявекторов);
(ассоциативность сложениявекторов);
(iii)  (нулевой вектор
(нулевой вектор 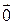 является нейтральным элементом относительно сложения);
является нейтральным элементом относительно сложения);
(iv) для любого вектора  V (E3) существует противоположный вектор
V (E3) существует противоположный вектор 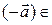 V (E3), т.е. такой, что
V (E3), т.е. такой, что  .
.
Все утверждения теоремы легко следуют из определения суммы векторов. Докажем, например, пункт (iv). Действительно, для любого вектора 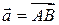 противоположным вектором является вектор
противоположным вектором является вектор  так как
так как  С алгебраической точки зрения теорема 1.2.1 означает, что множество всех векторов пространства V (E3) относительно операции сложения является абелевой группой.
С алгебраической точки зрения теорема 1.2.1 означает, что множество всех векторов пространства V (E3) относительно операции сложения является абелевой группой.
Используя понятие противоположного вектора, определим обычным образом операцию вычитания (разности) в множестве векторов.
Определение 1.2.2. Если  и
и 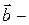 произвольные векторы, то разностью вектора
произвольные векторы, то разностью вектора  и вектора
и вектора  называется вектор
называется вектор 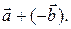
Разность вектора  и вектора
и вектора  обозначается
обозначается 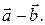 Из равенства треугольника (2) следует, что для любых точек
Из равенства треугольника (2) следует, что для любых точек 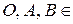 E3 верно равенство
E3 верно равенство
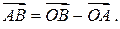 (3)
(3)
Упражнение 1.2.2. Докажите пункты (i) – (iii) теоремы 1.2.1.
Имея более чем два вектора  их можно последовательно сложить по формуле
их можно последовательно сложить по формуле  При этом будем использовать правило треугольника, т.е. отложим вначале вектор
При этом будем использовать правило треугольника, т.е. отложим вначале вектор 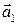 от точки
от точки  получив точку
получив точку 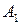 такую, что
такую, что  затем отложим вектор
затем отложим вектор  от точки
от точки  получив точку
получив точку 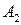 такую, что
такую, что  и т. д. (рис. 12).
и т. д. (рис. 12).

Рис. 12
В итоге получим ломаную 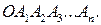 Сумма
Сумма  будет равна вектору
будет равна вектору  Такой способ построения суммы нескольких векторов называется правилом замыкающей (отрезок
Такой способ построения суммы нескольких векторов называется правилом замыкающей (отрезок 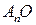 замыкает ломаную
замыкает ломаную  ). Сумму этих же векторов можно вычислить, расставляя скобки по другому, т.е. выполняя
). Сумму этих же векторов можно вычислить, расставляя скобки по другому, т.е. выполняя  раз операцию сложения в другом порядке. Свойство ассоциативности сложения векторов позволяет утверждать, что результат сложения всякий раз будет один и тот же. Поэтому можно не уточнять порядок выполнения сложения и обозначить вектор-сумму
раз операцию сложения в другом порядке. Свойство ассоциативности сложения векторов позволяет утверждать, что результат сложения всякий раз будет один и тот же. Поэтому можно не уточнять порядок выполнения сложения и обозначить вектор-сумму 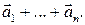
Упражнение 1.2.3. Докажите, что сумму трех некомпланарных векторов можно вычислить по правилу параллелепипеда: сумма векторов-ребер, выходящих из одной вершины параллелограмма равна вектору-диагонали, выходящему из этой же вершины:  (рис. 13).
(рис. 13).
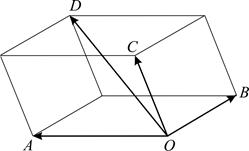
Рис. 13
Поскольку операция откладывания векторов плоскости от точек этой плоскости не выводит нас из плоскости, то сумма двух векторов плоскости E2 дает вновь вектор плоскости E2. Это означает, что определение 1.2.1 задает операцию сложения и в множестве V (E2) векторов плоскости E2. Легко видеть, что утверждения теоремы 1.2.1 остаются справедливыми при замене V (E3) на V (E2), т.е. множество V (E2) также является абелевой группой относительно операции сложения.
Все сказанное в предыдущем абзаце очевидно справедливо и для прямой, следовательно, определение 1.2.1 задает операцию сложения в множестве V (E1) векторов прямой E1 имножество V (E1) является абелевой группой относительно операции сложения.
Если 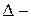 прямая,
прямая, 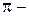 плоскость в пространстве E3, то, учитывая принятое выше соглашение о том, что V (
плоскость в пространстве E3, то, учитывая принятое выше соглашение о том, что V (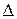 )
) 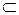 V (E3) и V (
V (E3) и V (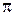 )
) 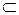 V (E3), можно утверждать, что V (
V (E3), можно утверждать, что V (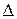 ) и V (
) и V (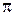 ) являются подгруппами группы V (E3).
) являются подгруппами группы V (E3).
Теперь перейдем к операции умножения векторов на числа.
Определение 1.2.3. Пусть  произвольный вектор,
произвольный вектор,  произвольное вещественное число. Произведением вектора
произвольное вещественное число. Произведением вектора  на число
на число  называется вектор, который обозначается
называется вектор, который обозначается 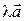 и определяется следующими условиями:
и определяется следующими условиями:
(i) 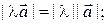
(ii) 
Из условия (i) следует, что вектор 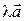 нулевой тогда и только тогда, когда вектор
нулевой тогда и только тогда, когда вектор  нулевой или число
нулевой или число  равно нулю. Отметим также, что для любого числа
равно нулю. Отметим также, что для любого числа  векторы
векторы  и
и 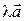 коллинеарны.
коллинеарны.
Если вектор  является вектором некоторой плоскости
является вектором некоторой плоскости 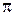 или некоторой прямой
или некоторой прямой 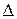 , то умножение на число не выводит вектор из соответствующего множества. Другими словами:
, то умножение на число не выводит вектор из соответствующего множества. Другими словами:
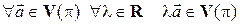 и
и

Операция умножения вектора на число обладает следующими основными свойствами.
Теорема 1.2.2. Для любых векторов  и для любых чисел
и для любых чисел 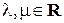 верны равенства:
верны равенства:
(i) 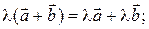
(ii) 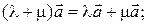
(iii) 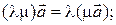
(iv) 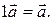
Доказательство. Равенство (iv) очевидно следует из определения 1.2.2.
Равенство (iii) вытекает из того, что векторы в правой и левой частях имеют одну и ту же длину  и одинаково направлены (их направление совпадает с направлением вектором
и одинаково направлены (их направление совпадает с направлением вектором  , если числа
, если числа  и
и 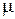 одного знака и противоположно направлению вектора
одного знака и противоположно направлению вектора  , если числа
, если числа  и
и 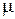 разных знаков).
разных знаков).
Равенство (ii) доказывается аналогично (iii) путем сравнения длин и направлений векторов в левой и правой частях; читателю предлагается провести рассуждение самостоятельно.
Равенство (i) докажем в общем случае, т. е. когда векторы  и
и  не коллинеарны и число
не коллинеарны и число  не равно нулю. Отложим векторы
не равно нулю. Отложим векторы  и
и  от некоторой точки
от некоторой точки 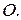 Получим соответственно точки
Получим соответственно точки 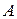 и
и 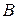 такие, что
такие, что  треугольник (рис.14).
треугольник (рис.14).

Рис. 14
Отложим также векторы 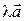 и
и 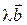 от точки
от точки 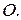 Получим соответственно точки
Получим соответственно точки 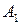 и
и 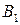 такие, что
такие, что  треугольник. Очевидно, треугольник
треугольник. Очевидно, треугольник  подобен треугольнику
подобен треугольнику  и коэффициент подобия равен
и коэффициент подобия равен 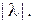 Записывая равенство отношений длин соответствующих сторон и учитывая знак числа
Записывая равенство отношений длин соответствующих сторон и учитывая знак числа  получаем:
получаем:

Учитывая равенство (3), последнее соотношение можно переписать в виде
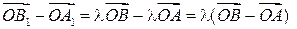 или
или 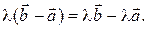
Таким образом, для любых неколлинеарных векторов  и
и  и любого ненулевого числа
и любого ненулевого числа  верно равенство
верно равенство 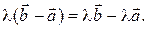 Заменяя в нем вектор
Заменяя в нем вектор  на
на  , получаем:
, получаем:  что и требовалось доказать. В случаях, когда векторы
что и требовалось доказать. В случаях, когда векторы  и
и  коллинеарны, или
коллинеарны, или 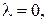 доказательство предлагается провести читателю в качестве упражнения.
доказательство предлагается провести читателю в качестве упражнения.
Замечание 1.2.1. Тот факт, что операции сложения векторов и умножения векторов на вещественные числа удовлетворяют утверждениям теорем 1 и 2 на языке линейной алгебры означает, что 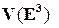 является вещественным векторным пространством.
является вещественным векторным пространством.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 1083; Нарушение авторских прав?; Мы поможем в написании вашей работы!