Проекции

Пусть 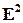– плоскость, 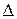и 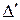– непараллельные прямые на плоскости. Если 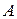– произвольная точка плоскости, то прямая 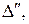проходящая через точку 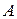параллельно 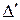, пересекает прямую 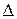в точке 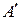(рис. 3.1).

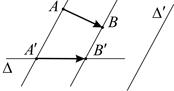
Рис. 3.1 Рис. 3.2

Определение 1.4.1. Точка 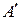называется проекцией точки 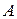на прямую 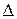параллельно прямой .

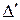Проекцию точки 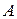будем обозначать следующим образом: 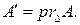Проекция называется ортогональной,еслипрямые 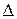и 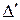ортогональны. В этом случае 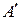– основание перпендикуляра, опущенного из точки 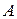на прямую .

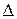[1] Давид Гильберт (1862 – 1943) – немецкий математик.

[2] Подробное изложение аксиоматики Гильберта имеется в книгах: Гильберт Д., Основания геометрии, пер. с нем. М. – Л., 1948; Ефимов Н.В., Высшая геометрия, 6 изд., М., 1978. Гильбертовская аксиоматика планиметрии обсуждается в книге Кононов С.Г., Тышкевич Р.И., Янчевский В.И., Введение в математику, ч. 2, Минск, 2003.

[3] Герман Вейль (1885 – 1955) – немецкий математик. Построение элементарной геометрии на основе аксиоматики Вейля проведено, например, в книге Болтянский В.Г., Волович М.Б., Семушин А.Д, Векторное изложение геометрии, Москва, "Просвещение", 1982 г.

[4] В преподавании школьной математики был период, когда учитывались эти нюансы и два равных (в используемой ныне терминологии) треугольника назывались конгруэнтными. Однако затем с точки зрения методики преподавания это усложнение терминологии было признано нецелесообразным.

[5] Подробнее о понятии направления см. [ ], стр. 79.

[6] См. [ ], § 1.9.

[7] О понятии направления см. [ ], § 1.9.

Дата добавления: 2014-11-09