Основные сведения об электромагнитных переходных процессах 2 страница

На рис. 3.3 справа показана векторная диаграмма токов в момент КЗ, а также изменения токов в зашунтированном участке схемы до и после короткого замыкания.

Очевидно, что в общем случае свободные токи в фазах различны, хотя их затухание, разумеется, происходит с одной и той же постоянной времени. В одной из фаз свободный ток может вообще отсутствовать, если в момент КЗ предшествовавший ток в этой фазе проходил через ноль. При этом свободные токи в двух других фазах будут одинаковы по величине, но противоположны по знаку.

Рассмотрим процессы, происходящие в цепи, которая осталась подключенной к источнику питания.

Для фазы А этого участка справедливо следующее уравнение

. (3.4)

Поскольку, , то

, (3.5)

где - результирующая индуктивность фазы А.

Аналогичные уравнения должны быть записаны и для фаз В и С. Тогда в общем виде для любой фазы участка, подключенного к источнику, можно записать

. (3.6)

Решение этого уравнения имеет вид

,

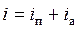где i_п - принужденный ток, обусловленный действием приложенного от источника напряжения;

i_a - свободный (апериодический) ток.

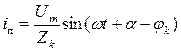; . (3.7)

В (3.7) - полное сопротивление цепи, оставшейся подключенной к источнику напряжения;

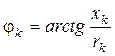- аргумент полного сопротивления этой цепи, или угол сдвига тока от напряжения в этой цепи;

α - фаза включения, т.е. угол, определяющий значение напряжения в фазе А в момент времени t =0.

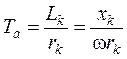. (3.8)

Ток i_п представляет периодическую слагающую, которая в рассматриваемых условиях является вынужденным (принужденным) током с постоянной амплитудой 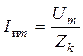. Ток i_a - это затухающий по экспоненте свободный апериодический ток. Его начальное значение 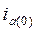определяется из начальных условий в соответствии с первым законом коммутации: ток в индуктивности не может изменяться скачком. Тогда,

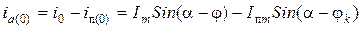, (3.9)

где 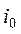- мгновенное значение тока предшествующего режима в момент включения выключателя (цепь: );

- мгновенное значение принужденного тока в цепи , оставшейся подключенной к источнику, в момент включения выключателя.

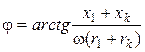; ; . (3.10)

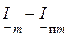Построим векторную диаграмму токов в начальный момент короткого замыкания. Она показана на рис. 3.4. В зависимости от фазы включения α меняется начальное значение от нуля (когда вектор параллелен линии времени) до некоторого наибольшего значения, когда этот вектор нормален к ней. Очевидно, что в общем случае все начальные значения свободных токов в фазах разные. Изобразим осциллограмму токов.

На рис.3.5 приведена осциллограмма изменения токов в фазе А.

Из рис.3.5 видно, что апериодическая составляющая является криволинейной осью симметрии изменения полного тока. Наибольшее мгновенное значение полного тока КЗ зависит от тока предшествующего режима и от фазы включения . При отсутствии тока исходного режима, величина может достигать амплитуды периодической принужденной слагающей, если в момент КЗ эта составляющая проходит через свой положительный или отрицательный максимум. Однако максимум апериодической составляющей не предопределяет того, что в этом случае будет максимальным мгновенное значение полного тока КЗ. Этот максимум называют ударным током.

Максимум полного тока (ударный ток) является функцией двух переменных и и определяется выражением

. (3.11)

Приравняв нулю частные производные и 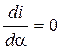и решив совместно эти уравнения найдем, что ударный ток наступает при условии . Следовательно, в предварительно разомкнутой цепи с индуктивностью ударный ток при КЗ наступает, если в момент возникновения КЗ мгновенное значение напряжения источника равняется нулю.

На рис.3.6. показана осциллограмма токов в фазе А, когда в момент КЗ апериодическая составляющая имеет наибольшее значение, т.е. принужденный ток в момент повреждения проходит через амплитудное значение.

Для цепей с преобладающей индуктивностью угол 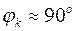, поэтому условие действительные возникновения ударного тока близки к условиям, когда апериодический ток имеет наибольшее значение. Поэтому в практических расчетах значение ударного тока i_у, обычно определяют при наибольшем значении апериодической составляющей (рис.3.6). Из рис.3.6 следует, что ударный ток наступает через полпериода промышленной частоты, т.е. через 0,01 сек. после возникновения КЗ. Таким образом, выражение для расчета ударного тока можно записать в следующем виде:

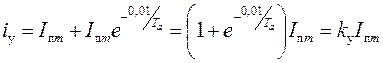, (3.12)

или

,

где I _П - действующее значение принужденного тока.

Ударный коэффициент показывает превышение ударного тока над амплитудой периодической составляющей.

При () .

При () .

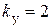Следовательно, . Естественно, чем меньше постоянная времени, тем быстрее затухает апериодическая слагающая и тем соответственно меньше ударный коэффициент. Зависимость ударного коэффициента от постоянной времени затухания приведена на рис. 3.7.

Для высоковольтных систем значение с. Это соответствует величине ударного коэффициента, равного 1,8. Следует обратить внимание на то, что апериодические составляющие токов в фазах различны. Поэтому определение трехфазного короткого замыкания как симметричного, строго говоря, справедливо к периодическим слагающим токов.

Тема №4:

«УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПЕРЕХОДНОГО ПРОЦЕССА СИНХРОННОЙ МАШИНЫ»

План:

4.1 Общие указания.

4.2 Исходные уравнения.

4.3 Обобщенный (изображающий) вектор трехфазной системы.

4.4 Замена переменных.

4.5 Уравнения Парка-Горева.

4.1 Общие указания

Рассмотрим так называемую “идеализированную машину”. Отметим часть дополнительных допущений, кроме уже упомянутых ранее.

1. Потери в магнитной системе машины отсутствуют.

2. Конструктивное выполнение машины обеспечивает полную симметрию обмоток статора и ротора.

3. Рассматриваются только первые гармоники кривых распределения намагничивающей силы и индукции в воздушном зазоре машины.

4. Все демпферные обмотки по осям ротора или массив турбогенератора представляются по одной эквивалентной в каждой из осей.

Таким образом, рассматриваем идеализированный СГ, на статоре которого расположены три обмотки (фазы А, В, С), сдвинутые в пространстве на угол 120^о (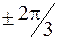). Ротор имеет две оси магнитной симметрии: продольную ось d и поперечную – q. Электрическая схема рассматриваемого СГ показана на рис.4.1.

Магнитное сопротивление СМ с явновыраженными (гидрогенераторы) полюсами по осям магнитной симметрии неодинаковые вследствие разного воздушного зазора между статором и ротором. Магнитное сопротивление СМ с неявновыраженными полюсами (турбогенераторы) по осм d и q практически одинаково. На роторе расположена обмотка возбуждения (обмотка f) и короткозамкнутая демпферная обмотка, которую представим двумя эквивалентными демпферными контурами, расположенными по одной по каждой из осей d и q (контуры 1 d 1 q). Ротор вращается с угловой скоростью 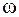. Положение ротора в расточке статора характеризуется углом между магнитной осью фазы А статора и осью d ротора. Этот угол является функцией времени;

,

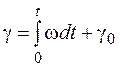где - начальное значение угла .

Если угловая скорость вращения ротора генератора постоянная и равная синхронной , то

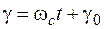. (4.1)

К обмотке возбуждения подведено постоянное напряжение 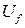от независимого источника. Его величину можно регулировать с помощью автоматического регулятора возбуждения (АРВ). Демпферные обмотки закорочены. Фазные токи статора генератора замыкаются через внешнюю цепь. СГ приводится в движение первичным двигателем, который развивает на валу машины положительный вращающий момент М.

4.2 Исходные уравнения

Рассмотрим трехфазную синхронную машину с демпферной обмоткой (рис.4.1). Стрелками показаны принятые положительные направления токов, напряжений и ЭДС в обмотках статора и ротора. Они выбраны таким образом, чтобы активная мощность, которую отдают обмотки статора СГ во внешнюю цепь, и активная мощность, которую потребляет ОВГ, были положительными.

Дифференциальные уравнения равновесия ЭДС и падений напряжений, составленные в соответствие со вторым законом Кирхгофа в каждой из обмоток будут иметь вид:

, , (4.2-4.4)

, (4.5)

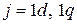. (4.6-4.7)

В (4.2) - (4.7) 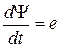- ЭДС, которые, в соответствии с законом электромагнитной индукции, индуктируются в цепи при изменении полного потокосцепления этой цепи.

Раскроем выражения для потокосцеплений, которые линейно зависят от токов (машина ненасыщенная). Обмотки СМ индуктивно связаны. Поэтому потокосцепления контуров определяются по формулам

,

,

,

,

,

,

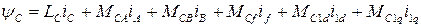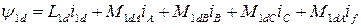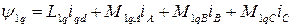где - собственные индуктивности обмоток статора и контуров, расположенных на роторе;

- взаимные индуктивности между фазными обмотками статора;

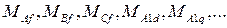- взаимные индуктивности между фазными обмотками статора и контурами, расположенными на роторе;

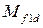- взаимная индуктивность между обмоткой возбуждения и продольной демпферной обмоткой.

Поскольку магнитная проницаемость магнитопровода СМ принимается равной бесконечности, то в соответствии с принципом взаимности и т.д. Магнитная связь между обмотками, расположенными взаимно перпендикулярно отсутствует: т.е. .

Большинство индуктивностей вращающейся машины зависят от положения ротора относительно обмоток статора и, следовательно, в исходных уравнениях имеются переменные коэффициенты.

Выясним закономерности изменения индуктивностей обмоток синхронной машины. Положение ротора будем фиксировать углом между магнитной осью фазы А статора и продольной осью d ротора.

Можно выделить три группы индуктивностей.

1. Индуктивности обмоток, расположенных на роторе.

2. Взаимные индуктивности между обмотками, расположенными на роторе и статоре.

3. Индуктивности обмоток, расположенных на статоре.

1. Индуктивности не зависят от положения ротора, а значит и от времени.

2. Взаимные индуктивности и др. зависят от положения ротора и определяются изменением электромагнитной связи между указанными обмотками. Следовательно, изменяться они будут с периодом 2 (один оборот). Максимум (M_d) наступает когда магнитные оси совпадают. Значит

.

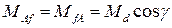Аналогичные зависимости будут иметь место и для взаимных индуктивностей между обмотками статора и расположенными по поперечной оси ротора.

.

Изменение индуктивностей фазных обмоток 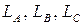и взаимных индуктивностей определяются изменением магнитной проводимости зависящей только от расположения ротора. Значит они будут изменяться с периодом . При разложении в ряд Фурье эквивалентных кривых изменения рассматриваемых индуктивностей он будет иметь только четные гармоники (т.е. функция не зависит от знака ) Для фазы А, например, имеем

; .

По физической сущности . Индуктивности максимальны когда , т.е. ; .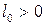

Взаимные индуктивности фазных обмоток отрицательны т.к. углы между магнитными осями больше . При индуктивность максимальна, а при 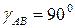- минимальна. Тогд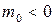а , а 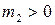. Причем, .

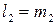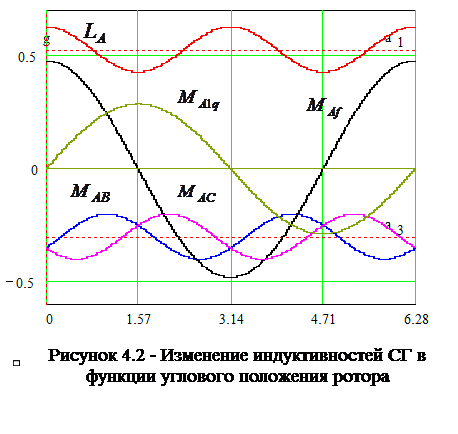На рис.4.2 приведены зависимости изменения индуктивностей СГ, от углового положения ротора.

4.3 Обобщенный (изображающий) вектор трехфазной системы

Мгновенные значения переменных (токов, напряжений и др.) можно получить проектируя три вращающихся вектора, которыми характеризуется трехфазная система, на неподвижную ось времени. Те же значения можно получить если векторы оставить неподвижными, а вращать линию времени в противоположном направлении с той же скоростью (рис.4.3,а) Мгновенные значения можно так же получить, проектируя единый (обобщенный) вращающийся вектор на три неподвижные оси времени. При его вращении против часовой стрелки чередование осей времени фаз нужно изменить на противоположные. Однако, с помощью обобщенного вектора можно представить любые мгновенные значения, изменяющиеся во времени по любому закону при условии, что 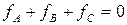. Это связано с тем, что сумма проекций вектора на три оси, сдвинутые на угол 120⁰ всегда будет равна нулю. Такой вектор называется обобщенным или изображающим вектором трехфазной системы. При известных мгновенных величинах 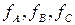значение модуля обобщенного вектора определяется как

.

Положение этого вектора можно охарактеризовать углом 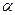по отношению к оси фазы А (рис.4.3,а):

.

4.4 Замена переменных

Попробуем произвести замену переменных таким образом, чтобы в дифференциальных уравнениях освободиться от переменных коэффициентов. Такое преобразование впервые предложил Блондель для установившегося режима СГ.

Изображающий вектор можно проектировать не на неподвижные оси трехфазной системы, а на любые другие оси. В качестве таких осей выберем продольную и поперечную оси ротора, которые вращаются вместе с ротором (рис.4.3,б).

Такое преобразование по существу математических операций соответствует замене переменных

,

.

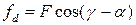Связь с фазными переменными определяется следующими равенствами:

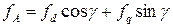, (4.8)

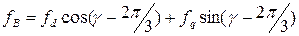, (4.9)

. (4.10)

Решив систему уравнений (4.8) – (4.10) относительно 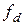и , имеем

,

.

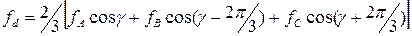Если сумма мгновенных значений не равна нулю, то добавляется еще одна составляющая .

.

В этом случае при переходе к фазным переменным необходимо в каждом из равенств (4.8) – (4.10) добавлять нулевую составляющую .

Под переменной f можно понимать ток, напряжение, потокосцепление и др.

Трехфазная система, например, токов, которая изменяется по закону косинуса, в системе вращающихся координат d, q изображается постоянными величинами. Действительно, поскольку обобщенный вектор, модуль которого равен амплитудному значению тока, вращается с синхронной скоростью в направлении вращения ротора, то проекция этого вектора на оси d, q – величины постоянные.

4.5 Уравнения Парка-Горева

Преобразуем дифференциальное уравнение, записанное для статорной обмотки, например фазы А СГ, (4.3), путем замены фазных переменных их составляющими в координатах d, q.

.

После перегруппировки слагаемых это выражение можно представить в следующем виде

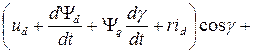
(4.11)

.

Уравнение (4.11) должно быть справедливо при любых значения . Это возможно только при условии, что каждое из слагаемых (4.11) заключенных в скобки тождественно равны нулю. Следовательно, выражение (4.11) распадается на три уравнения:

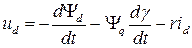, (4.12)

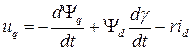, (4.13)

. (4.14)

Уравнения для обмоток, расположенных на роторе (4.5) – (4.7) не изменятся.

В (4.12), (4.13) составляющие и - ЭДС трансформации. Они возникают при изменении соответствующего потокосцепления, связанного с изменением токов. В установившемся режиме при постоянных значениях токов ЭДС трансформации отсутствуют.

Составляющие 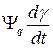и - ЭДС вращения. Они возникают при перемещении магнитного потока, вызванного вращением ротора.

В соответствии с (4.1) . При синхронной скорости вращения ротора в относительных единицах получим .

Полученные уравнения (4.12) – (4.14) вместе с уравнениями (4.5-4.7) называют полными уравнениями Парка-Горева. Им можно дать такую физическую интерпретацию. Три неподвижные фазные обмотки статора заменили двумя эквивалентными обмотками вращающимися вместе с ротором, и в которых протекает ток i_d и i_q. Магнитные оси этих обмоток направлены вдоль осей d и q. Электрическая схема такого преобразованного синхронного генератора пока зана на рис.4.4

Таким образом, по продольной оси имеем три неподвижные относительно друг друга контура (эквивалентная статорная обмотка d, обмотка возбуждения f и продольна демпферная обмотка 1d), связанные общим потоком взаимоиндукции . По поперечной оси имеем два контура (эквивалентная статорная обмотка q и поперечная демпферная обмотка 1q), связанных потоком взаимоиндукции 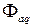. Токи, протекающие в каждом контуре создают магнитные потоки рассеяния 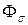, связанные только с соответствующей обмоткой. Поскольку оси d и q ортогональны, то магнитные связи между контурами, расположенными по этим осям, отсутствуют.

В соответствии с выполненными преобразованиями выражения для результирующих потокосцеплений обмоток синхронного генератора будут иметь вид

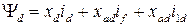, (4.15)

, (4.16)

, (4.17)

, (4.18)

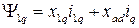, (4.19)

. (4.20)

Поскольку в преобразованной машине обмотки, расположенные по каждой из осей магнитной симметрии не перемещаются относительно друг друга, то в уравнениях (4.15) - (4.20) для потокосцеплений постоянные коэффициенты.

Тема №5:

«Установившийся режим короткого замыкания синхронной машины»

План:

5.1 Общие указания.

5.2 Решение уравнений СГ для установившегося симметричного режима.

5.3 Физическая модель процесса.

5.4 Влияние и учет нагрузки.

5.5 Влияние автоматического регулирования возбуждения.

5.6 Практический расчет тока установившегося КЗ в цепи, которая питается от генераторов без АРВ.

5.7 Расчет тока КЗ в цепи, которая питается от генератора с АРВ.

Литература: Л1 – с. 91-111, Л2 – с. 69-71, Л3 – с. 76-86.

5.1 Общие указания

Установившийся режим трехфазного КЗ соответствует такой стадии переходного процесса, когда свободные составляющие токов практически затухли, а изменение тока возбуждения от действия АРВ закончено. Такой режим условный, поскольку он возникает только при автономной изолированной работе генератора.

Дата добавления: 2014-11-16