Уравнение Клапейрона-Менделеева

Как уже указывалось, состояние некоторой массы определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния.

Французский физик Б.Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля-Мариотта и Гей-Люссака.

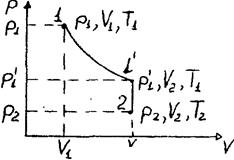Рис. 49

Пусть некоторая масса газа занимает объем V1, имеет давление p1 и находится при температуре T1. Эта же масса газа в другом произвольном состоянии характеризуется параметрами р2, V2, T2 (рис. 49). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов:

1) изотермического (изотерма 1-1¢),

2) изохорного (изохора 1¢-2).

В соответствии с законами Бойля-Мариотта (1.1) и Гей-Люссака (1.4) запишем:

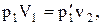(1.5)

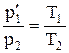.(1.6)

Исключив из уравнений (1.5) и (1.6) p₁', получим

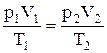
Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина 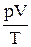остается постоянной, т.е.

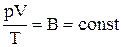. (1.7)
Выражение (1.7) является уравнением Клапейрона, в котором В - газовая постоянная, различная для разных газов.

Русский ученый Д.И.Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (1.7) к одному молю, использовав молярный объем V_m. Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем V_m, поэтому постоянная В будет одинакова для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению

PV_m=RT (1.8)

удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Менделеева-Клапейрона.

Числовое значение молярной газовой постоянной определим из формулы (1.8), полагая, что моль газа находится при нормальных условиях (р₀=1,013×10⁵ Па, Т₀=273,15 К, V_m=22,41×10^-3 м³ /моль): R=8,31 Дж/(моль К).

От уравнения (1.8) для моля газа можно перейти к уравнению Клапейрона-Менделеева для произвольной массы газа. Если при некотором заданном давлении и температуре один моль газа занимает объем V_m, то при тех же условиях масса m газа займет объем 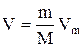, где М - молярная масса (масса одного моля вещества). Единица молярной массы - килограмм на моль (кг/моль). Уравнение Клапейрона-Менделеева для массы m газа

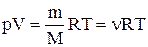, (1.9)

где 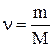- количество вещества.

Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:

.

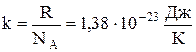Исходя из этого, уравнение состояния (1.8) запишем в виде

,

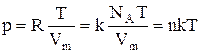где 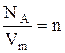- концентрация молекул (число молекул в единице объема). Таким образом, из уравнения

р=nkT (1.10)
следует, что давление идеального газа при данной температуре прямо пропор-ционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м³ газа при нормальных условиях, называется числом Лошмидта:

.

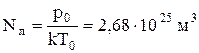Дата добавления: 2014-11-16