Правила записи международного символа точечной группы

Сингония	Позиция в символе	Пример записи
1-я	2-я	3-я	Полное	Краткое
Триклинная	Один символ, соответствующий любому направлению в кристалле
Моноклинная	Единственная ось 2׀׀ Y или плоскость m ^ Y или
Ромбическая	Ось 2 или плоскость m вдоль X	Ось 2 или плоскость m вдоль Y	Ось 2 или плоскость m вдоль Z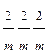
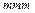
Тригональная^*	Ось 3 или ׀׀ Z	Ось 2 ׀׀ X, Y или плоскость m ^ X, Y		3 m	3 m
Гексагональная	Ось 6 или ׀׀ Z или 6 ׀׀ Z и m ^Z	Ось 2 ׀׀ X, Y или плоскость m ^ X, Y	Ось 2 ׀׀ диагональ­ному направлению или плоско­сть m ^ ей
Тетрагональная	Ось 4 или ׀׀ Z или 4 ׀׀ Z и m ^Z	Ось 2 ׀׀ X, Y или плоскость m ^ X, Y	Ось 2 ׀׀ диагональ­ному направлению или плоско­сть m ^ ей
Кубическая	Ось 4 или ׀׀ X, Y, Z или m ^ X, Y, Z	Ось 3 или под углом 45^о по отношению к осям X, Y, Z	Ось 2 ׀׀ диагональ­ному направлению или плоско­сть m ^ ей

* В ромбоэдрической установке основная ось 3 расположена вдоль [111], оси 2 или плос­кости m вдоль трех направлений и трех .

В моноклинной сингонии одно особое направление, поэтому бу­дет занята одна позиция. Чтобы показать, как ориентирован кристалл, по двум другим позициям следует расположить оси первого порядка 1.

В триклинной сингонии нет особых направлений, в обозначении группы один символ: поворотная или инверсионная ось первого порядка.

В группах средней категории на первом месте располагается символ, обозначающий особое направление – ось высшего порядка: 3, 4, 6; на втором – побочное координатное направление, совпадающее с осями X и Y; на третьем – особое направление, образующее с побочными координатными направлениями угол α /2, где α –

элементарный угол поворота главной оси.

В группах высшей категории обязательно наличие четырех осей 3-го порядка и символ этих осей 3 записывается на второй позиции, на первой указывается символ особых координатных направлений, на третьей – символ особых диагональных направлений.

В символике Бравэ приняты следующие обозначе­ния: плоскость симметрии Р, центр симметрии С, оси симметрии L₁, L ₂, L ₃, L ₄, L ₆, инверсионные оси симметри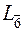и , , , , или , , , , .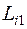

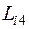В формуле класса симметрии выписы­ваются подряд все элементы симметрии — сначала оси, начиная с высших порядков, затем плоскости, затем центр. Так, например, символ L ₆7PC означает: одна ось L ₆, 7 плоскостей симметрии, центр симметрии. По теореме 4 вдоль оси L ₆ может проходить лишь шесть плоскостей, значит, седьмая плоскость симметрии должна отли­чаться по расположению от остальных шести; наличие центра сим­метрии С () показывает согласно теореме 2, что эта плоскость перпендикулярна к оси L ₆ (6). Аналогично читаются остальные фор­мулы симметрии.

Наглядная и простая символика Браве не является общепринятой в связи с тем, что она громоздка, не привязана к системе координат, не описывает всех особенностей симметричных преобразований (правые или левые повороты и др.)

В символике Шенфлиса применяются следующие обозначения: С_п — одна ось симметрии порядка n; D_n — одна ось симметрии порядка п и п осей 2, перпендикулярных к ней. Единственная ось всегда считается вертикальной, т. е. осью Z. Если осей несколько, то вертикальной считается ось высшего порядка.

Индексы v, h и d обозначают плоскости симметрии, добавленные к вертикальной оси, соответственно: v — вертикальные, h — горизонтальные, d— диагональные. Если имеются оба типа плоскостей, в символ вставля­ются только координатные.

Буква Т означает совокупность осей симметрии кубического тетраэдра, О — совокупность осей симмет­рии кубического октаэдра.

Таким образом, С_п — одна вертикальная полярная ось порядка n, C_nv — одна вертикальная полярная ось порядка п и п плоско­стей симметрии, проходящих вдоль нее, С_пh — одна ось п и пло­скость симметрии, перпендикулярная к ней, D_n — одна вертикаль­ная ось порядка п и п осей 2, перпендикулярных к ней, D_nh — одна вертикальная ось порядка n, плоскость симметрии к ней перпен­дикулярная и п осей симметрии 2, а также те плоскости симметрии, которые порождаются при пересечении этих элементов, например, D_4h = 4/ mmm; S_n — одна вертикальная зеркально-поворотная ось порядка п (иногда применяют знак C_ni, где i — знак инверсионной оси: S (S₍₁₎) = , S ₂ = С_i = , S ₃ = C_3h = 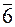, S₄ = , S ₆ = C_3i= ), – одна вертикальная инверсионная ось порядка п; V = D₂ - сочетание трех взаимно перпендикулярных осей второго порядка, V_h = D_2h – три взаимно перпендикулярные, оси 2 и плоскости, перпендикулярные к каждой из этих осей; V_d = D_2d – три взаимно перпендикулярные оси 2 и диагональные плоскости; Т – оси сим­метрии тетраэдра, Т_d — оси симметрии тетраэдра и диагональные плоскости, Т_h — оси симметрии тетраэдра и координатные плоско­сти; О — оси симметрии октаэдра, O_h — оси симметрии октаэдра и координатные плоскости.

Дата добавления: 2014-11-16