Предельные группы симметрии (группы Кюри)

Укрупненные группировки кристаллов

Кроме деления на сингонии 32 класса симметрии можно группировать по более крупным объединениям в зависимости от характерных элементов симметрии.

1. Наличие или отсутствие центра симметрии. В центральных и планаксиальных классах не может быть полярных направлений, поэтому не может быть свойств, характеризуемых полярной симметрией; остальные 21 класс – ацентрические.

2. Энантиоморфизм. Кристаллы, принадлежащие к классам, в которых есть только поворотные оси симметрии, но нет инверсионных осей, поперечных плоскостей и центра симметрии, могут иметь правые и левые разновидности. Энантиоморфными являются примитивные и аксиальные классы.

3. Лауэвские классы симметрии. Согласно закону Фриделя, или закону центросимметричности дифракционного эффекта, из-за симметрии отражения рентгеновских лучей дифракционная симметрия кристалла выше, чем его точечная симметрия. Она отвечает точечной группе плюс центр инверсии и плюс элементы симметрии, порождаемые из-за добавления центра инверсии.

В отличие от числа точечных групп симметрии, описывающих кристаллические вещества, число точечных групп симметрии, которыми могут описываться конечные физические системы, бесконечно. Среди этого множества групп большое значение, наряду с кристаллографическими, имеют группы, содержащие оси симметрии бесконечного порядка. Такая симметрия характерна для физических полей, тел вращения и некоторых физических свойств кристаллов.

Точечные группы, содержащие оси симметрии бесконечного порядка, называются предельными группами симметрии, или группами Кюри. Кюри показал, что имеется 7 предельных точечных групп. Симмет­рия каждой из них наглядно изобра­жается соответствующей геометричес­кой фигурой (рис. 5.5).

а)	б)	в)	г)
	д)	е)	ж)
Рис. 5.5. Геометрические фигуры, символизирующие группы симметрии П.Кюри: а) ∞, правая и левая; б) ∞ m; в) ∞/ m; г) ∞ 2, правая и левая; д) ∞/ mтт; е) ∞∞, правая и левая; ж) ∞/∞ m

1. Группа ∞ содержит только од­ну ось симметрии бесконечного по­ряд­ка. Ей соответствует равномерно вра­щающийся круговой конус. Группа по­лярна и энантиоморфна, потому что конус может вращаться вправо и вле­во. Очевидно, группа ∞ является пре дельной для кристаллографических групп 6, 4, 3, 2, 1.

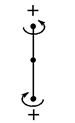
2. Группа ∞ m, т. е. имеется ось симметрии бесконечного порядка и беско­нечное число продольных плоскостей симметрии. Ее символизирует покоя­щийся круговой конус. Группа полярна, но не энантиоморфна. Такова симметрия однородного электрическо­го поля: вектор его напряженности Е можно изобразить полярной стрелкой (рис. 5.6, а), положительный и отрица­тельный заряды физически различны, поэтому концы стрелки несовмес­тимы, нет и не может быть поперечных элементов симметрии. Вдоль стрелки проходит бесконечное число продольных плоскостей симметрии.

а)	б)	в)	г)	д)	е)
Рис. 5.6. Графическое пояснение понятий полярности и аксиальности направлений: а — полярное; б — аксиальное; в, г — биаксиальные; д, е — биполярные

3. Группа ∞ /т, т. е. имеются ось бесконечного порядка, поперечная плос­кость симметрии и центр инверсии. Это симметрия вращающегося цилиндра. Торцы цилиндра неодинаковы.

Их можно различить, глядя на цилиндр с торца: с одной стороны мы видим, что вращение совершается по часовой стрелке, с другой — против часовой стрелки. Однако ось симметрии здесь не полярна: оба ее конца можно совместить друг с другом путем отражения в поперечной плоскости сим­метрии.

Цилиндр, вращающийся вправо, можно совместить с цилиндром, вра­щающимся влево, отражая его в име­ющемся центре инверсии или просто перевернув и наложив один на дру­гой, без отражения. Поэтому в этой группе нет энантиоморфных форм.

4. Группа ∞2 содержит ось симмет­рии бесконечного порядка и бес­конеч­ное число поперечных осей 2 и может быть представлена цилиндром, концы которого закручены в разные стороны. В этой группе возможен энан­тиоморфизм.

Такая симметрия характерна для удельного вращения плоско­сти поля­ризации в анизотропной среде: неза­висимо от того, как смотреть на ци­линдр, снизу или сверху, правое вра­щение оста­ется правым, левое — ле­вым.

5. Группа ∞/ттт, изобра­жаемая покоящимся цилиндром (рис. 5.5, д) или стрелкой с двумя одина­ковыми концами (рис. 5.6, в, г), со­держит одну ось бесконечного порядка, одну поперечную и бесконечное мно­жество продольных плоскостей сим­метрии, бесконечное множество про­дольных осей 2 и центр симметрии. Та­кова симметрия одноосного сжимаю­щего или растягивающего механического усилия.

6. Группа ∞/∞ описывает сим­мет­рию обычного шара (рис. 5.5, е); имеется центр симметрии и бес­конечное множество осей бесконечного по­рядка и плоскостей симметрии. Это симмет­рия таких скалярных воздей­ствий, как гидростатическое сжатие или однородный нагрев.

7. Последняя, седьмая, группа ∞/∞ т включает в себя беско­нечное множество осей симметрии бес­конечного порядка, без плоскостей и центра симметрии. Изображают ее своеоб­разным шаром (рис. 5.5, ж), у кото­рого все диаметры за­кручены по пра­вому или левому винту соответствен­но правой или левой энантиоморфной формам. Такова симметрия удельного вращения плоскости поляриза­ции в изотропной среде.

32 точечные группы симмет­рии кри­сталлических многогран­ников являют­ся подгруппами семи предельных групп.

[1] В таблицах выделены группы или полученные ранее, или которые относят к другим классам симметрии.

Дата добавления: 2014-11-16