Вывод точечных групп симметрии

Установлено, что возможны 32 комбинации различных группировок элементов симметрии или 32 кристаллографических класса или вида симметрии. Данные 32 класса симметрии были сначала выведены математическим путем в 1830 году И.Гесселем, а затем независимо от него в 1867 году русским академиком А.В.Гадолиным.

Для вывода 32 классов симметрии необходимо рассмотреть все возможные сочетания кристаллографических элементов симметрии, пересекающихся в одной точке. Для этого выбирается исходный порождающий элемент симметрии и к нему добавляются поочередно все остальные элементы симметрии в качестве порождающих.

Рассмотрим кристаллы, имеющие особенные направления т.е., относящиеся к низшей и средней категориям. Выберем в качестве порождающего элемента симметрии ось симметрии, проходящую вдоль особенного направления, и будем добавлять к ней другие элементы симметрии (рис.5.3).

Плоскости симметрии могут проходить лишь вдоль выбранной оси или перпендикулярно к ней, так как при другом расположении ось симметрии, отразившись в плоскости симметрии, повторится, т.е. не будет единственной. По этой же причине оси 2 могут быть только перпендикулярны к выбранной оси. Центр симметрии может располагаться только на выбранной оси. Поэтому никаких сочетаний, кроме представленных на рис.5.3 в кристаллах низшей и средней категорий быть не может.

а)	б)	в)
г)	д)	е)
Рис. 5.3. Порождающие комбинации элементов симметрии в средней и низшей категории

Примем за начальную порождающую комбинацию простую ось симметрии (рис.5.3, а), получаем 5 примитивных классов симметрии:

Символика	Браве	L 1	L 2	L 3	L 4	L 6
Шенфлиса	С 1	С 2	С 3	С 4	С 6
Германа-Могена
Стереографическая проекция

К оси симметрии добавляем центр симметрии (рис.5.3, б). В случае осей четного порядка это приводит к формированию плоскости симметрии, перпендикулярной оси. В случае оси нечетного порядка эквивалентно действию инверсионной оси. При этом получаем 5 центральных классов симметрии:

Символика	Браве	C	L 2 PC	L 3 C	L 4 PC	L 6 PC
Шенфлиса	С i	С 2h	С 3i	С 4h	С 6h
Германа-Могена
Стереографическая проекция

Комбинируя поворотную ось и перпендикулярную к ней ось симметрии 2-го порядка (рис.5.2, г) получаем 5 аксиальных классов:

Символика	Браве	L 2	3 L 2	L 33 L 2	L 44 L 2	L 66 L 2
Шенфлиса	С 2	D 2	D 3	D 4	D 6
Германа-Могена
Стереографическая проекция

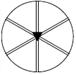
Добавляя к порождающей оси симметрии проходящую через нее плоскость симметрии (рис.5.3, в), получаем 5 планальных класса:

Символика	Браве	Р	L 22 Р	L 33 Р	L 44 Р	L 66 Р
Шенфлиса	С s	C 2v	C 3v	C 4v	C 6v
Германа-Могена	m	mm 2	3 m	4 mm	6 mm
Стереографическая проекция

Если к порождающей оси симметрии добавить центр, ось 2 и продольную плоскость (рис.5.3, е), то получим 5 планаксиальных класса:

Символика	Браве	L 22 РС	3 L 23 РС	L 33 L 23 РС	L 44 L 25 РС	L 66 L 27 РC
Шенфлиса	С 2h	D 2h= V h	D 3d	D 4h	D 6h
Германа-Могена	2 /m	mmm		4/ mmm	6/ mmm
Стереографическая проекция

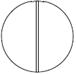
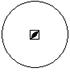
Совмещая единичное направление с осью инверсии, получаем 5 инверсионно-примитивных класса:

Символика	Браве	С	Р	L 3 С	L 4i	L 3 Р
Шенфлиса	С i= S 2	C s= C 1h	C 3i= S 6	S 4	C 3h
Германа-Могена
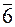
Стереографическая проекция

Если к порождающей инверсионной оси добавить плоскости симметрии, проходящие вдоль оси, то получаем 4 инверсионно-планальных класса:

Символика	Браве		3 L 23 РC	L 33 L 23 РС	L 42 L 22 Р	L 33 L 24 Р
Шенфлиса		D 2h= V h	D 3d	D 2d	D 3h
Германа-Могена		mmm
Стереографическая проекция

Примечание (см. ссылку)[1]

Добавление других элементов симметрии приводит к одной из уже имеющихся комбинаций. Таким образом, у кристаллических многогранников, обладающих единичным направлением, имеется всего 27 классов симметрии.

В кристаллах высшей категории нет особенных направлений и может быть несколько осей симметрии порядка более 2, пересекающихся в одной точке. Можно показать, что в этих кристаллах возможны два сочетания осей симметрии: 4, 3, 2 и 3, 3, 2, которые соответствуют осям симметрии октаэдра (или куба) и осям симметрии тетраэдра (рис.5.4).

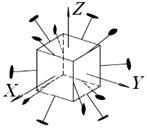
а)	б)
Рис. 5.4. Возможные сочетания осей симметрии в кристаллах высшей категории: а – октаэдра или куба; б – тетраэдра

Соответственно получаем два класса симметрии кубической сингонии: примитивный (оси симметрии тетраэдра), аксиальный (оси симметрии тетраэдра или куба).

Класс симметрии	Примитивный	Центральный	Аксиальный	Планальный	Планаксиальный
Символика	Браве	4 L 33 L 2	4 L 33 L 23 РС	3 L 44 L 36 L 2	3 L 44 L 36 Р	3 L 44 L 36 L 2 9 РС
Шенфлиса	Т	Тh	О	Тd	Oh
Германа-Могена		m 3			m 3 m
Стереографическая проекция

Добавляя к системе осей группы тетраэдра центр симметрии, получаем центральный класс симметрии.

Добавляя к системе осей группы тетраэдра плоскости симметрии, проходящие через одну ось симметрии 2-го порядка и две оси 3-го порядка, получим планальный класс.

Аксиальный класс получаем, добавляя к системе осей группы тетраэдра оси симметрии 2-го порядка, перпендикулярные осям симметрии 3-го порядка, при этом ранее существовавшие оси 2-го порядка становятся осями симметрии 4-го порядка.

Планаксиальный класс получаем, добавляя к системе осей группы октаэдра центр симметрии.

Дата добавления: 2014-11-16