Лекция 12

.

.

.

.

Рис. 16.

Уравнение, относительно которого дисперсия минимальна, называется уравнением регрессии. Рассматривая дисперсию как функцию от двух переменных a и b воспользуемся необходимым условием экстремума

Решая эту систему относительно a и b, получим

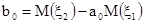, , уравнение регрессии - у = 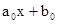(Рис.16),

при этом дисперсия , и она является минимальной.

Таким образом, уравнение регрессии у = 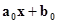, дает наилучшее линейное представление ξ₂ по ξ₁.

Количественной характеристикой нелинейной взаимосвязи случайных величин ξ₁, ξ₂ является корреляционное отношение. Коэффициент корреляционного отношения ξ₂ по ξ₁ вычисляется по формуле:

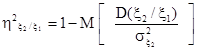, (30)

где 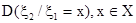- условная дисперсия, характеризующая рассеяние ξ₂ около условного математического ожидания .

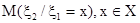Свойства корреляционного отношения:

1. .

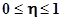2. η=0 соответствует некоррелированным случайным величинам.

3. η=1,тогда и только тогда, когда имеет место функциональная зависимость между ξ₁ и ξ₂. В случае линейной зависимости ξ₂ от ξ₁ корреляционное отношение совпадает с квадратом коэффициента корреляции.

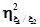Корреляционное отношение несимметрично относительно ξ₁ и ξ₂, поэтому наряду с рассматривается , определяемое аналогичным образом. Между и 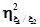нет какой-либо простой зависимости.

Теперь рассмотрим совокупность n-случайных величин 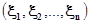.Можно вычислить коэффициенты корреляции ρ_ij между каждой парой случайных величин. Они составят корреляционную матрицу

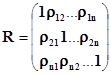
ρ_ij=ρ_ji, i≠j т.е. матрица симметрична относительно главной диагонали.

Взаимосвязь какой-либо случайной величины ξ_i со всеми остальными случайными величинами характеризуется множественным коэффициентом корреляции

(31)

|R| - определитель матрицы R,

R_jj – алгебраическое дополнение, соответствующее элементу корреляционной матрицы ρ_jj,

.

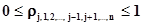Дата добавления: 2014-11-16