
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сили пружності
|
|
|
|
Із дослідів відомо, що під час пружних деформацій механічне напруження прямо пропорційне до відносної деформації:
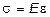 , (3.3)
, (3.3)
де коефіцієнт пропорційності Е називають модулемЮнга (Т. Юнг (1773–1829) – англійський учений). Одиниця вимірювання модуля Юнга - [Н/м2].
Із (3.3) випливає, що модуль Юнга чисельно дорівнює напруженню, яке спричинює відносне видовження стрижня, що дорівнює одиниці.
Підставимо в (3.3) праві частини рівнянь (3.1) і (3.2):
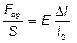 . (3.4)
. (3.4)
З останньої рівності знайдемо сумарну пружну силу
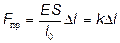 , (2.3.5)
, (2.3.5)
де k = ES / l 0.
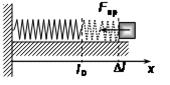 У рівнянні (3.5) врахуємо знаком "–" такий експериментальний факт: під час деформації твердого тіла в ньому виникають сили пружності F пр, які завжди напрямлені проти зовнішніх сил, що зумовлюють деформацію (рис. 3.2): рис. 3.2
У рівнянні (3.5) врахуємо знаком "–" такий експериментальний факт: під час деформації твердого тіла в ньому виникають сили пружності F пр, які завжди напрямлені проти зовнішніх сил, що зумовлюють деформацію (рис. 3.2): рис. 3.2
 , (3.6)
, (3.6)
де k - коефіцієнтпружності. Рівність (3.6) є математичним записом закону Гука: сила пружності F пр, яка виникає в разі малих деформацій, прямо пропорційна до значення деформації D l і протилежна до неї за напрямом.
Із рис. 3.3 бачимо, що визначена англійським ученим Р. Гуком (1635–1703) лінійна залежність (3.6) виконується лише у вузьких межах – до так званої межі пропорційності sп. За подальшого збільшення напруження деформація ще пружна, але вже не лінійна. Тому до межі пружності sпр залишкові деформації не виникають. За межею пружності в тілі виникають залишкові деформації, і тіло після припинення дії на нього зовнішньої сили не повертається у початковий стан. Напруження, за якого виникає помітна залишкова деформація (» 0,2 %),
рис. 3.3
називають межеютекучості (sт). На графіку s(e) їй відпові-дає горизонтальна ділянка, яка відображає, що деформація тіла зростає без збільшення напруження – тіло ніби “тече”. Цю область називають областю текучості (або областю пластичної деформації). З подальшим збільшенням напруження тіло руйнується. Максимальне напруження, яке виникає в тілі до руйнування, називають межеюміцності sм.
 Матеріали, для яких область текучості значна, називають в’язкими, а в яких її практично нема – крихкими.
Матеріали, для яких область текучості значна, називають в’язкими, а в яких її практично нема – крихкими.
|
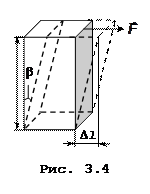
 відбувається деформація зсуву (здеформований паралелепіпед показано штриховими лініями). Відносну деформацію зсуву визначають за формулою
відбувається деформація зсуву (здеформований паралелепіпед показано штриховими лініями). Відносну деформацію зсуву визначають за формулою
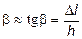 , (3.7)
, (3.7)
де D l – абсолютний зсув шарів тіла один відносно одного; h – відстань між шарами. Кут b називають відносним зсувом. Формула (3.7) застосовна для малих кутів b, де справджується співвідношення tgb» b.
Деформації розтягу (стиску) і зсуву належать до однорідних деформацій, за яких усі малі елементи тіла деформовані однаково. До неоднорідних деформацій належать деформації кручення і згину. У цих випадках деформація всередині тіла у різних точках різна.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 614; Нарушение авторских прав?; Мы поможем в написании вашей работы!