Iмпульс. Закон збереження імпульсу

З урахуванням того, що в класичній механіці m = const, перепишемо другий закон Ньютона:

. (4.1)

Вектор , який дорівнює добутку маси матеріальної точки на її швидкість, називають імпульсомматеріальної точки. З (4.1) випливає, що другий закон Ньютона можна сформулювати так: швидкість зміни імпульсу матеріальної точки дорівнює силі, що діє на неї.

З рівності (4.1)

, (4.2)

де – зміна імпульсу матеріальної точки; 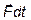– імпульс сили.

На підставі дослідних даних сформульовано принцип незалежності дії сил (принципсуперпозиції сил): якщо на матеріальну точку (точкове тіло) діє одночасно декілька сил, то кожна з них надає матеріальній точці такого прискорення, як у випадку відсутності інших сил. Математичний запис такий:

. (4.3)

Тобто 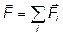- це рівнодійна всіх сил, що діють на матеріальну точку.

Розглянемо замкнуту систему тіл. Тіла, що не належать системі, називатимемо зовнішнім середовищем. Розрахуємо, як змінюється імпульс замкнутої системи, що складається з n точкових тіл, яка поміщена в зовнішнє середовище з деякою кількістю точкових тіл.

Для і -ї матеріальної точки системи другий закон Ньютона набуде такого вигляду:

, (4.4)

де m_i та – відповідно, маса та швидкість і -ї матеріальної точки; 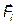– рівнодійна всіх сил, що діють на неї.

Назвемо зовнішніми тісили, що діють на тіла системи з боку зовнішнього середовища, а внутрішніми – сили взаємодії між тілами системи. Тоді рівнодійна всіх сил, що діють на і -ту матеріальну точку, дорівнює геометричній сумі всіх зовнішніх сил 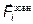, що діють на цю матеріальну точку, та рівнодійної всіх внутрішніх сил:

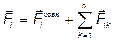, (4.5)

де 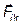– сила, яка діє з боку k -го точкового тіла системи на і -те тіло системи.

З урахуванням (4.5) рівняння (4.4) набуде такого вигляду:

.

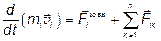Підсумуємо всі сили в цьому рівнянні, щоб знайти сумарний імпульс системи:

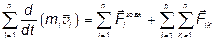. (4.6)

За третім законом Ньютона 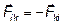, тобто , звідки випливає, що . Вектор називають головним (рівнодійним) вектором усіх зовнішніх сил.

Iмпульсом механічної системи називають вектор, що дорівнює геометричній сумі імпульсів усіх матеріальних точок цієї системи:

. (4.7)

Рівняння (4.6) з урахуванням (4.7) і третього закону Ньютона набуде такого вигляду:

. (4.8)

Це основний закондинаміки поступального руху механічної системи.

На практиці важливе значення мають ізольовані та замкнені системи. Iзольованою системою називають групу тіл, що взаємодіють одне з одним і не взаємодіють з іншими тілами (зовнішнім середовищем). Тобто це система, яка не взаємодіє з зовнішнім середовищем – вона не обмінюється з зовнішніми тілами ні речовиною, ні енергією. Замкненою називають систему, яка ізольована механічно, тобто не може обмінюватись із зовнішнім середовищем енергією шляхом виконання роботи (взаємодії тіл системи з зовнішніми тілами нема).

На тіла замкненої системи зовнішні сили не діють (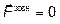), тому другий закон Ньютона запишемо так:

. (4.9)

Із (4.9) випливає, що . Це законзбереження імпульсу: сумарний імпульс усіх тіл замкненої механічної системи – стала величина.

Закон збереження імпульсу можна записати в іншому вигляді:

, (4.10)

де 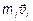, - імпульс і -го тіла системи до та після взаємодії, відповідно. Отже, сума всіх імпульсів тіл системи до взаємодії дорівнює сумі всіх імпульсів тіл системи після взаємодії.

Дата добавления: 2014-11-16