Метод четырехугольников без диагоналей

Сети четырехугольников без диагоналей, заполняя каркас, создают сплошную сеть (рис.49). Все пункты этой сети взаимно связаны и своей формой эта сеть напоминает строительную сетку. Так как диагональные направления не измеряются, то этот метод с успехом используется на застроенных и залесенных площадках.

Рисунок 49 – Схема построения четырехугольников без диагоналей

При расчете точности измерений в сети, уравненной между пунктами каркаса, можно использовать таблицу 7.

Таблица 7

Система построения Sx = Sy	Q	QSx	Qax	QSy	Qay
3x3 3x4 3x5 4x3 4x4 4x5 5x3 5x4 5x5	0,59 0,67 0,71 0,76 0,67 0,81 0,71 0,81 0,86	0,60 0,76 0,84 0,59 0,76 0,84 0,59 0,77 0,86	0,41 0,41 0,41 0,44 0,45 0,45 0,46 0,47 0,47	0,59 0,59 0,59 0,72 0,76 0,77 0,84 0,84 0,86	0,41 0,44 0,46 0,41 0,45 0,47 0,41 0,45 0,47

Нормированные обратные веса вычислены для наиболее слабых элементов сети, независимо от конкретной длины ее сторон. При этом приняты следующие обозначения:

Q -корень из нормированного обратного веса положения пункта в самом слабом месте сети;

Q_Sx, Q_Sy - то же - для длин соответствующих сторон;

Q_ax, Q_ay - то же - для дирекционных углов этих сторон.

Переход к сети с конкретными длинами сторон осуществляется по формулам:

; ;

; ;

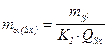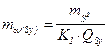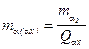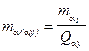где m_S2 и m_a2 - требуемая точность длин сторон и дирекционных углов этих сторон.

В заполняющих сетях m_S=10 мм, m_a=10².

Из этих четырех значений выбирают минимальное и вычисляют ошибку положения пункта:

M_II =K₁× m_a(min)× Q, K₁ =S/r";

где S - длина стороны строительной сетки в мм.

Дата добавления: 2014-11-16