Микротриангуляция

Микротриангуляцию строят для определения координат пунктов строительной сетки из цепочек между исходными сторонами полигонометрии 1-го порядка (риc. 50). В результате получают взаимосвязанные элементы двух рядов пунктов сетки. Недостаток метода заключается в том, что отсутствует взаимная связь между смежными цепочками. Поскольку обычно все цепочки имеют одинаковую протяженность и форму, при составлении проекта достаточно рассчитать требуемую точность измерений один раз.

Рисунок 50 – Схема построения цепочек микротриангуляции

Угловые измерения в сети выполняют по трех штативной системе. Для расчета их точности и оценки точности уравненных элементов сети можно использовать табл. 8 (по аналогии с табл. 7).

Таблица 8

Система построения	Число треугольников	Q	QSx	Qax	QSy	Qay	QS	Qa
Sx = Sy		1,1 1,5 1,8	0,94 1,0 1,1	0,66 0,78 0,82	0,72 0,80 0,84	0,61 0,65 0,72	0,9 1,3 1,6	1,3 1,7 2,0
Sx = Sy/ 2		1,4 1,5 1,6	1,4 1,5 1,6	0,66 0,80 0,80	0,84 1,0 1,1	1,2 1,3 1,4	1,0 1,5 1,7	1,8 2,1 2,4

Примечание: Q_S и Q_a - корни из нормированных обратных весов длины и дирекционного угла стороны между пунктами соседних цепочек в их середине.

Рассмотрим примеры расчета точности сети, принимая, как и в примерах для метода четырехугольников без диагоналей, те же исходные данные.

Пример 1. Число треугольников n=10, сетка квадратов S₁ = S₂=S= 200 м, m_S2 =±10 мм, ma₂ =±10", M=±40 мм, К₁ =0.97.

Для обеспечения требуемой точности определения длин сторон имеем:

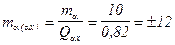²; ²;

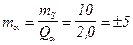²; ²;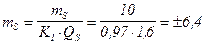

²; ²;

Приняв за окончательный более жесткий допуск m_{a (min)} = ± 5" получим ошибку положения пункта:

M = K₁×m_a(min)×Q = 0,97×5×1,8 = ±8,7 мм.

При уравнивании цепочки микротриангуляции между сторонами полигонометрии 1-го порядка применяют коррелатный способ. Отнеся в первую группу условия фигур и введя первичные поправки путем распределения невязок поровну, для нахождения вторичных поправок решают систему из четырех нормальных уравнений коррелат, соответствующих условиям базиса, дирекционных углов, абсцисс и ординат. Свободные члены этой системы находят по первично исправленным углам.

Дата добавления: 2014-11-16