Характеристики динамічних рядів

Для оцінки динаміки розвитку різних суспільних явищ статистика використовує взаємозв'язані характеристики, або аналітичні показники. Серед них: абсолютний приріст, темп зростання, темп приросту і абсолютне значення 1 % приросту. Складовими динамічного ряду є ознака часу (t)– момент, або інтервал і числові значення показника – рівні .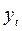

Розрахунок характеристики динаміки ґрунтується на зіставленні рівнів ряду. Базою для зіставлення може бути або попередній рівень а6o початковий – .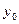

Характеристики динаміки, обчислені зіставленням суміжних значень рядів звуться ланцюговими, а з постійною базою порівняння – базисними.

Розглянемо показники ряду динаміки.

1. Абсолютний приріст (зменшення) 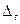як різниця рівнів ряду

а) базисний ;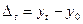

б) ланцюговий ,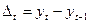

де 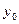— початковий рівень;

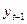— попередній рівень.

Ланцюгові та базисні абсолютні прирости адитивно пов'язані між собою сума ланцюгових приростів дорівнює кінцевому базисному.

,

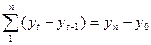де 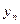- кінцевий рівень ряду.

2. Темп зростання К, розраховується як відношення рівнів і виражається у відносних числах (індекси, проценти)

а) базисний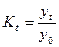

б) ланцюговий

Добуток ланцюгових темпів зростання дорівнює кінцевому базисному.

,

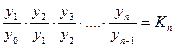де – кінцевий базисний індекс.

3. Темп приросту 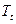виражається в процентах і показує наскільки рівень y_t більший (менший) від рівня, взятого за базу порівняння.

а) базисний ;

б) ланцюговий .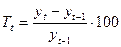

Між темпом приросту і темпом зростання існує такий зв'язок:

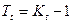, або .

4. Абсолютне значення 1% приросту A_t характеризує вагомість кожного проценту приросту і розраховується тільки на ланцюговій основі, так як на базисній основі для всіх рівнів буде одне і те саме значення показника - сота частина базисного рівня.

.

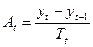Цей показник має практичне значення в економічному аналізі. При зростанні рівнів динамічного ряду, темпи зростання можуть навіть сповільнюватися, а значення одного проценту приросту зростати

До складу аналітичних показників можна віднести коефіцієнт прискорення(уповільнення) – 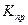, який розраховується як відношення двох сусідніх темпів зростання – та 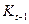, визначених ланцюговим способом:

.

При порівнянні динаміки розвитку двох явищ можна використати показник, який являє собою відношення темпів зростання за однакові проміжки часу за двома динамічними рядами. Цей показник називається коефіцієнтом випередження :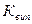

,

де 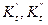відповідно темп зростання порівнюваних рядів динаміки.

З допомогою цього коефіцієнту можна зіставляти ряди динаміки різного змісту, які характеризують один і той же об'єкт (темп зростання обсягу виробленої продукції і вартість основних засобів).

Для узагальнення оцінок швидкості та інтенсивності змін динамічного ряду використовують середні величини. До середніх аналітичних показників відносяться: середній рівень динамічного ряду (цей показник розглянуто на початку теми), середній абсолютний приріст, середній темп зростання, середній темп приросту.

Середній абсолютний приріст 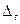характеризує середню швидкість зростання рівнів ряду:

,

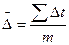де m — число ланцюгових абсолютних приростів (m=n-l).

Середній темп зростання розраховують за формулою середньої геометричної:

,

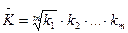де 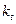темп зростання за окремі періоди часу

або

,

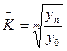де 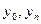початковий та кінцевий рівні ряду динаміки.

Середній темп приросту 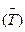показує на скільки процентів у середньому збільшується (зменшується) цей рівень порівняно з попереднім:

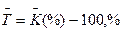
Приклад. Існують такі дані про виробництво в Україні валового внутрішнього продукту (ВВП).

Таблиця 7.3 – Виробництво ВВП в Україні

Роки
Валовий внутрішній продукт, млрд.грн.	267,3	345,1	441,5	544,2	712,9

Розрахувати: аналітичні та середні показники динаміки.

Таблиця 7.4 – Аналітичні показники

Роки	ВВП, млрд.грн	Абсолютний приріст, млрд.грн.	Темп зростання, %	Темп приросту, %	Абсолютне значення 1 % приросту, млрд.грн.
Баз.	Ланц.	Баз.	Ланц.	Баз.	Ланц.	Баз.	Ланц.
	267,3		• • •	100,0	• ••		• ••	• • •	• • •
	345,1	77,8	77,8	129,11	129,11	29,11	29,11	2,673	2.673
	441,5	174,2	96,4	165,17	127,93	65,17	27,93	2,673	3,451
	544,2	276,9	102,7	203,59	123,26	103,59	23,26	2,673	4,415
	712,9	445,6	168,7	266,70	131,00	166,70	31,00	2,673	5,442

Середні показники.

1.Середнійрівень виробництва ВВП:

.

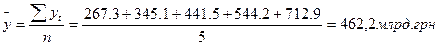2.Середній абсолютний приріст:

.

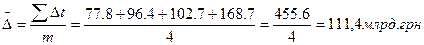3. Середній темп зростання:

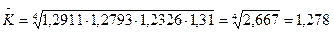або 127,8%

або

або 127.8%.

4. Середній темп прирост:

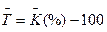T=127.8-100.00=27.8%.

Дата добавления: 2014-11-16