Оцінка щільності

Оцінка щільності зв'язку – це оцінка узгодженості варіації взаємозв'язаних ознак. Для оцінювання щільності зв'язку статистика використовує низку коефіцієнтів з такими спільними властивостями:

- за відсутності будь-якого зв'язку значення коефіцієнта наближається до нуля, при функціональному зв'язку – до одиниці;

- за наявності кореляційного зв'язку коефіцієнт виражається дробом, який за абсолютною величиною тим більший, чим щільніший зв'язок.

Для лінійного зв'язку використовується лінійний коефіцієнт кореляції Пірсона – r. Обчислення лінійного коефіцієнта кореляції – r ґрунтується на відхиленнях значень взаємозв'язаних ознак х і у від середніх:

За даними табл. 6.2:

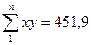
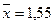
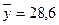
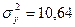
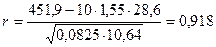
Величина коефіцієнта кореляції свідчить про досить значний вплив кількості внесених добрив на врожайність зернових. Коефіцієнт кореляції характеризує не тільки щільність, а й напрям зв`язку. Додатнє значення свідчить про прямий зв`язок, а від'ємне – про зворотній.

Знаки коефіцієнтів кореляції і регресії однакові, величини їх взаємозв'язані функціонально:

; ;

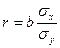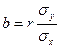Завдяки цьому один коефіцієнт можна обчислити, знаючи інші

;

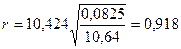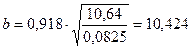
Вимірювання щільності нелінійного зв'язку групується у співвідношенні варіацій теоретичних та емпіричних (фактичних) значень результативної ознаки у. Як відомо, відхилення індивідуального значення ознаки у від середньої 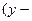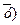можна розкласти на дві складові.

У регресійному аналізі це відхилення лінії регресії від середньої 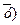, то є наслідком дії фактора х та відхилення фактичного значення від лінії регресії 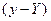, що є наслідком дії інших факторів.

Взаємозв'язок факторної та залишкової варіації описується правилом декомпозиції варіації:

,

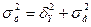де:

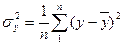– загальна дисперсія ознаки – у;

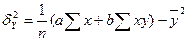– факторна дисперсія;

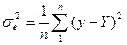– залишкова дисперсія.

Значення факторної дисперсії буде тим більшим, чим сильніший вплив фактора х на результат у.

Відношення факторної дисперсії до загальної розглядається як міра щільності кореляційного зв’язку і називається коефіцієнтом детермінації:

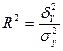
За попередніми розрахунками:

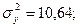
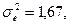то ,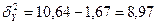

або

.

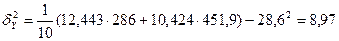Коефіцієнт детермінації становить:

,

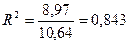тобто 84,3% варіації врожайності зернових залежить від варіації кількості внесених добрив, а 15,7% припадає на інші фактори.

Корінь квадратний з коефіцієнта детермінації називають індексом кореляції R. Коли зв’язок лінійний R=|r|, що підтверджують обчислення:

.

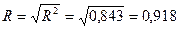Тому за відомим лінійним коефіцієнтом кореляції r можна визначити внесок ознаки х -у варіацію у. Так при r = 0,8 можна сказати, що 64% варіації у залежить від варіації х.

У моделі аналітичного групування мірою щільності зв’язку є відношення міжгрупової дисперсії до загальної, яке називають кореляційним відношенням:

,

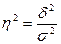де 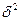– міжгрупова дисперсія, яка вимірює варіацію ознаки у під впливом тільки груповальної ознаки х;

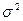– загальна дисперсія, яка вимірює варіацію результативної ознаки у, зумовлену впливом всіх можливих факторів.

Кореляційне відношення коливається від 0 до 1, а якщо подається в процентах, то від 0 до 100%. За відсутнього зв’язку 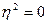, а за умови функціонального – 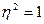.Чим більше наближається до одиниці, тим щільніший зв’язок.

Застосуємо кореляційне відношення для оцінки щільності зв’язку між розміром МТК і продуктивністю праці (див. табл.6.3 та 6.4). Розрахунок загальної та факторної дисперсії показано нижче. Згідно з розрахунками загальна дисперсія становить 4,41, а факторна 2,69.

Таблиця 6.3 – (до розрахунку загальної дисперсії продуктивності праці

())

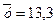Продуктивність праці, тонн молока на 1 особу	до 10	10-12	12-14	14-16	16 і більше	Разом
Кількість господарств -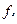
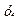
						х
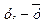
	-4,3	-2,3	-0,3	1,7	3,7	х
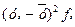
	92,4	58,2	2,2	52,0	82,1	286,9

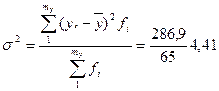
Таблиця 6.4 (до розрахунку загальної дисперсії продуктивності праці

())

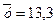Кількість корів,голів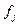
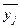
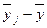
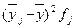
До 200		10,1	-3,2	92,16
200-400		12,8	-0,5	7,00
400-600		14,3		21,00
600 і більше		16,1	2,8	54,88
По сукупності в цілому		13,3	X	175,04

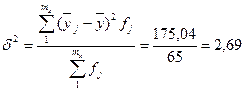
Кореляційне відношення:

,

тобто 61% варіації продуктивності праці на МТК пояснюється варіацією кількості корів.

Обчислення та інтерпретація коефіцієнта детермінації 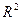і кореляційного відношення показують: ці характеристики щільності зв’язку за змістом ідентичні, вони характеризують внесок фактора х у загальну варіацію результату у.

Дата добавления: 2014-11-16