Обчислення дисперсії

Дисперсія посідає особливо місце в статистичному аналізі соціально-економічних явищ і є важливим елементом статистичних методів зокрема у дисперсійному аналізі. Для ознак метричної шкали дисперсія є базою для обчислення середнього квадратичного відхилення .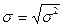

Дисперсія, на відміну від інших характеристик варіації є адитивною величиною. Тобто у структурованій сукупності, яка поділена на m груп за факторною ознакою х, загальна дисперсія 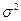результативної ознаки у, може бути розкладена на: дисперсію у кожній групі (внутрішньогрупову) та дисперсію між групами (міжгрупову).

Загальна дисперсія характеризує варіацію ознаки у за рахунок впливу всіх причин(факторів), міжгрупова – за рахунок фактору х, покладеного в основу групування, а внутрішньогрупові – за рахунок інших факторів, не врахованих у групуванні.

Внутрішньо групова дисперсія розраховується окремо для кожної j-ї групи:

,

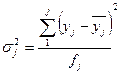де 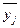– середня j-ї групи;

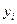– значення ознаки окремих елементів сукупності;

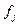– чисельність одиниць (частота) j-ї групи;

Для усіх груп в цілому розраховується середня з внутрішньогрупових дисперсій, зважених на частоти відповідної групи:

,

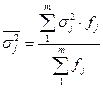де 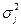– внутрішньогрупова дисперсія j-ї групи.

Міжгрупова дисперсія δ² (дельта) розраховується за формулою:

,

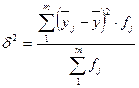де 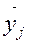та 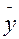– відповідно середня j- ї групи та загальна середня варіюючої ознаки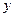

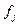- чисельність одиниць (частота) j-ї групи.

Взаємозв’язок між трьома дисперсіями дістав назву правила складання дисперсій, згідно яких:

.

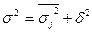Користуючись цим правилом можна за двома відомими дисперсіями знайти третю – невідому, а також мати уяву про силу впливу групувальної ознаки.

В умовах широкого застосування обчислювано техніки, зокрема ПЕОМ, зручніше вести обчислення дисперсій за формулою різниці квадратів:

,

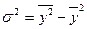де 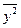– середній квадрат значень варіюючої ознаки,

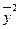– квадрат середньої величини.

Наведена формула дисперсії матиме такий вигляд для згрупованих даних^

.

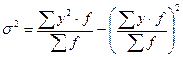Розрахунок зазначених дисперсій показано за даними табл. 5.8 на прикладі депозитних процентних ставок в окремих відділеннях банків, %.

Таблиця 5.8 – Депозитні процентні ставки 10 відділень банків

Відділення комерційних банків	Депозитні ставки в окремих відділеннях, %
Центральні					–	–
Філії

По даним табл. 5.8 визначимо групові, міжгрупову та загальну дисперсію процентної ставки і покажемо окремо їх зв’язок.

Складаємо робочу таблицю:

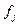
Відділення	Кількість відділень	Процентні ставки, % У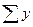
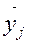
Центральні		16,22,20,18
Філії		25,31,33,28,27,24
В цілому		Х		24,4

Варіація депозитних процентних ставок для кожного відділення банку визначається двома внутрішньогруповими дисперсіями.

Для центральних відділень внутрішньогрупова дисперсія становить:

.

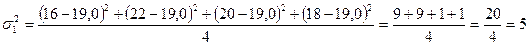Для філій:

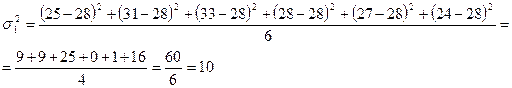
Середня з внутрішньогрупових дисперсій дорівнює

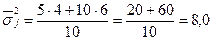
Для розрахунку міжгрупової дисперсії необхідно знати загальну середню варіюючої ознаки

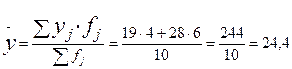
Розрахунок міжгрупової дисперсії:

,

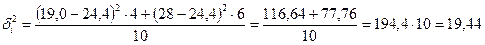де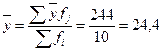

Загальна дисперсія як сума між групової та середньої з групових дисперсії:

.

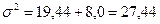Безпосереднє обчислення загальної дисперсії за спрощеною формулою:

.

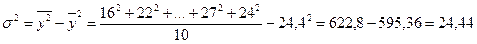Середнє квадратичне відхилення (зважене):

.

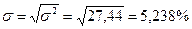Квадратичний коефіцієнт варіації:

.

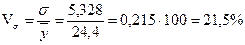Таким чином, сукупність є однорідною, а середня – типовою, так як коефіцієнт варіації не перевищує 33%.

Дата добавления: 2014-11-16