Мода і медіана

В статистичних рядах розподілу середніми величинами є мода і медіана, що відноситься до структурних середніх. Їх величини залежать лише від характеру частот, тобто від структури розподілу. Мода і медіана не залежать від крайніх значень ознаки, що важливе для незакритих крайніх інтервалів варіаційних рядів розподілу.

Мода (М₀) – це значення варіанти, що найчастіше повторюється в ряду розподілу. Для атрибутивних і дискретних рядів розподілу моду визначають візуально за значенням варіанти з найбільшою часткою (розряд робітників). В інтервальному ряду найперше визначається модальний інтервал (інтервал з найбільшою частотою) і значення моди в середині інтервалу розраховується за формулою:

,

де х₀ – нижня межа модального інтервалу;

h – величина модального інтервалу;

f₁ , f₂, f₃– частота відповідно передмодального, модального і після модального інтервалів.

Медіанною (М_е) називають варіанту, що ділить ранжируваний (впорядкований за мірою зростання чи зменшення) ряд на дві рівні за обсягом частини.

Медіана для дискретного ряду з непарним числом варіант буде відповідати середній варіанті М_е = x_m-1, де m – номер кратної варіанти першої половини ранжируваного ряду.

Медіана для дискретного ряду з непарним числом варіанти буде відповідати середній із значень варіант у ранжируваному ряду:

.

Для інтервального ряду медіана обчислюється для середини медіанного інтервалу, за який приймається такий, де сума накопичених частот перевищує половину значень частот ряду розподілу.

де х₀ – нижня межа медіанного інтервалу;

h – величина медіанного інтервалу;

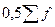– половина суми накопичених частот інтервального ряду;

– сума накопичених частот перед медіаним інтервалом;

f_m – частота медіанного інтервалу.

Приклад. За даними ряду розподілу працівників підприємства за стажем визначити структурні середні(модальний та медіанний) рівні, середній стаж працівників.

Таблиця 5.5 – Групування працівників по тривалості стажу роботи

Стаж, років	до 4-х	4–8	8–12	12–16	16 і більше	Всього
Число працівників

Розрахунок.

Таблиця 5.6 – Розрахунок структурних середніх

Стаж, років	Число працівників,	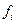x		Накопичені частоти ∑f
До 4-х
4 – 8
8 – 12
12 – 16
16 і більше
Всього		х		Х

Середній стаж роботи працівника:

.

Розрахунок моди виконується на підставі таких даних: частота модального інтервалу f₂ =46, яка є найбільшою із частот і відповідає інтервалу від 8 до 12 років, нижня межа модального інтервалу х₀=8, ширина модального інтервалу h=4; передмодальна частота f₁ =26, післямодальна – f₃ =14. Тоді модальне значення стажу працівників буде таким:

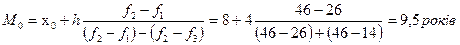
Для розрахунку медіани приймаємо, що перевищення половину обсягу сукупності відповідає іншому інтервалові від 8 до 12.Він і є медіанним інтервалом з частотою f_n=46; нижня межа медіанного інтервалу х₀=8; медіанний інтервал h=4; суманакопичених частот перед медіанним інтервалом .

Таким чином медіана стажу працівників складає:

.

Розрахунок показує, що без урахування крайніх значень в середині інтервального ряду середній стаж працівників складає 9,3 роки. А в модальному (найчастішому) інтервалі – 9,5 роки.

Таким чином, мода і медіана дозволяють знайти середні значення варіант варіаційного ряду з відкритими крайніми інтервалами. Оцінка їх значень може бути здійснена з визначенням середнього стажу.

Дата добавления: 2014-11-16