
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Относительное удлинение и сужение после разрыва образца
|
|
|
|
А б
а – вид диаграммы в координатах σ - 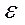 ;
;
б – вид кривой, отвечающей действительным напряжениям при растяжении низкоуглеродистой стали
Рисунок 2.2 – Вид диаграммы растяжения низкоуглеродистой стали в координатах: σ – 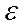 ,S – ψ
,S – ψ
Полное удлинение, полученное образцом после разрушения, умень-шится после разрыва, так как в его частях исчезнут упругие деформации. Относительным удлинением после разрыва δ называют отношение в про-центах прироста расчетной длины образца после разрыва к его начальной длине:
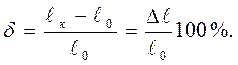 (2.6)
(2.6)
Относительное сужение образца после разрыва ψ определяется отно-шением абсолютного уменьшения площади поперечного сечения образца в процентах к начальной площади поперечного сечения:
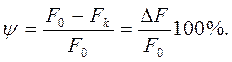 (2.7)
(2.7)
Относительное удлинение δ и относительное сужение ψ характери-  зуют пластичность материала и есть условными, так как удлинение и сужение относятся к первичной длине и к первичной площади образца. В действительности пластическая деформация развивается на непрерывно изменяющейся длине образца. Обозначив d
зуют пластичность материала и есть условными, так как удлинение и сужение относятся к первичной длине и к первичной площади образца. В действительности пластическая деформация развивается на непрерывно изменяющейся длине образца. Обозначив d 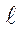 увеличение длины образца в данный момент испытания, находим истинное (действительное) удлинение:
увеличение длины образца в данный момент испытания, находим истинное (действительное) удлинение:
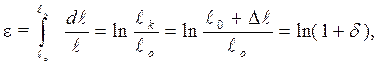 (2.8)
(2.8)
где δ = D 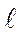 /
/ 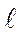 0.
0.
При разложении правой части в ряд по степеням δ получим:
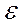 = ln(1+δ) = δ - δ2 + δ3 - …
= ln(1+δ) = δ - δ2 + δ3 - …
При малых изменениях δ условная и соответствующая ей действительная деформация практически совпадают. Так, при δ = 10% 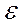 = 9,95%.
= 9,95%.
Подобным образом определяем действительное сужение:
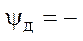
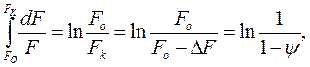 (2.9)
(2.9)
где ψ = DF/F0.
Так как объем тела во время пластической деформации не изменяет-ся, то F0 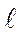 0 = Fk
0 = Fk 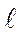 k, или
k, или 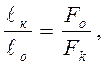 то есть
то есть 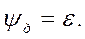
Любое увеличение длины относительно исходной базы образца вы-зовет соответствующее уменьшение диаметра базы образца.
Необходимость определения соответствующей действительной де-формации вытекает из факта, что она в любой заданный момент времени зависит от длины базы образца 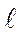 і в тот же момент времени. Таким обра-зом, фиксированное изменение длины D
і в тот же момент времени. Таким обра-зом, фиксированное изменение длины D 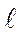 і приводит к постоянно умень-шаемому увеличению деформации, так как длина базы образца
і приводит к постоянно умень-шаемому увеличению деформации, так как длина базы образца 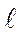 і в этот момент времени возрастает с каждым дополнительным увеличением D
і в этот момент времени возрастает с каждым дополнительным увеличением D 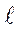 .
.
Кроме того, возможно определение действительной деформации стержня, если рассмотреть полное изменение его длины независимо от того, была ли эта деформация за счет одноразового растяжения или набором последовательных приложений нагрузки, то есть
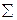
 полн =
полн =  общ,
общ,
где  общ – деформация при многоразовом прикладывании нагрузки.
общ – деформация при многоразовом прикладывании нагрузки.
Пример: растяжение стержня в два приема.
Сумма условных относительных деформаций (δ1+δ2) не будет равна величине общей относительной деформации (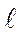 2 -
2 - 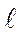 0) /
0) / 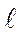 0:
0:
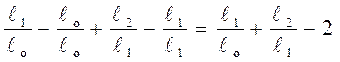 ,
,
а при сложении действительных деформаций ( 1 +
1 +  2) полная относи-тельная деформация
2) полная относи-тельная деформация  полн будет равняться
полн будет равняться  общ:
общ:
ln(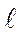 1/
1/ 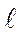 o) + ln(
o) + ln(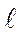 2 /
2 / 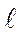 1) = ln(
1) = ln(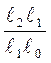 ) = ln(
) = ln(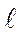 2 /
2 / 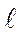 0) =
0) =  общ.
общ.
Деформации безразмерные. Отношение абсолютной продольной деформации элемента к его начальной длине в направлении оси Х носит название относительной продольной деформацией:
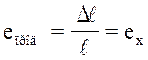 . (2.10)
. (2.10)
Отношение абсолютной поперечной деформации элемента к его начальному поперечному размеру носит название относительной попе-речной деформацией (рис.2.3):

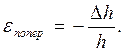 (2.11)
(2.11)
Коэффициент Пуассона 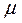 – абсолютное значение отношения отно-сительной поперечной деформации к относительной продольной деформа-ции при растяжении или сжатии на участке упругости, на котором дейст-вует закон Гука:
– абсолютное значение отношения отно-сительной поперечной деформации к относительной продольной деформа-ции при растяжении или сжатии на участке упругости, на котором дейст-вует закон Гука:
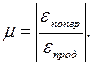 (2.12)
(2.12)

 Рисунок 2.3 – Поперечные деформации стержня
Рисунок 2.3 – Поперечные деформации стержня
Коэффициент поперечной деформации (коэффициент Пуассона) в пределах упругих деформаций:
μупр =  поп /
поп /  прод = (0,25...0,30);
прод = (0,25...0,30);  поп = –μупр
поп = –μупр  прод.
прод.
Полная деформация состоит из упругой и пластической:
 полн =
полн =  упр+
упр+  пл . (2.13)
пл . (2.13)
За пределом упругости увеличение продольных пластических дефор-маций вызовет поперечную деформацию с коэффициентом 0,5, в то время как увеличение упругих деформаций продолжает вызывать поперечные деформации с коэффициентом μ. За пределом упругости поперечная де-формация определяется по формуле
 поп = – (μ
поп = – (μ  прод +0,5
прод +0,5  пл). (2.14)
пл). (2.14)
Так как коэффициент Пуассона за пределом упругости μ' изменяет-ся по мере роста пластической деформации от μ до 0,5 (рис.2.4), то с рос-том пластической деформации отношение  пл /
пл /  полн стремится к едини- це, в то время как
полн стремится к едини- це, в то время как  упр /
упр /  полн стремится к нулю.
полн стремится к нулю.
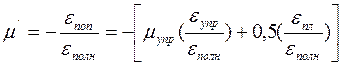 . (2.15)
. (2.15)
Секущий модуль, являющийся по аналогии с модулем упругости от-ношением 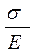 , обозначается
, обозначается 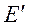 (см.рис.2.4). По мере роста пластической деформации он уменьшается, так как уменьшается угол
(см.рис.2.4). По мере роста пластической деформации он уменьшается, так как уменьшается угол 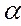 , образованный лучом ОА и осью
, образованный лучом ОА и осью  .
.
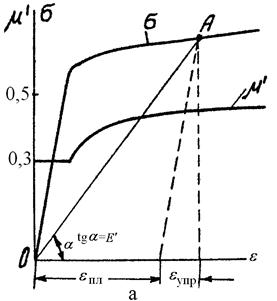
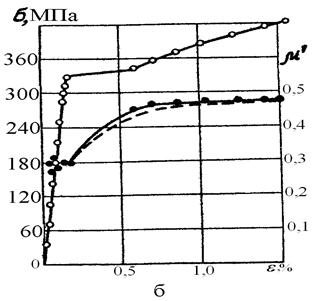
а - схема расчета μ' б – результаты для стали 30
Рисунок 2.4 – Диаграмма растяжения и графические зависимости коэффициента поперечной деформации от величины полной деформации
Закон неизменяемости объема металла при пластической деформации:
 хпл +
хпл +  упл +
упл +  zпл = 0, (2.16)
zпл = 0, (2.16)
где  хпл,
хпл,  упл,,
упл,,  zпл – соответствующие действительные пластичес-кие деформации в направлении координатных осей X,Y,Z.
zпл – соответствующие действительные пластичес-кие деформации в направлении координатных осей X,Y,Z.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 5370; Нарушение авторских прав?; Мы поможем в написании вашей работы!