Плоское напряженное состояние, плоская деформация

А б

Рисунок 2.12 – Диаграммы зависимости 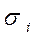от 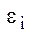(для обычных материалов) и 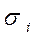от ∫ d 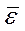_iпл ((для металлов с малым пределом

упругости), которыми пользуются в теории пластичности

Показатель степени n упрочнения материала при пластической де-формации для углеродистых и низколегированных сталей в неупрочнен-ном состоянии равен 0,25...0,30; для сталей высокой прочности -0,05…0,10. Повышение прочности металла обычно сопровождается умень-шением n. Неупрочняемый идеально упругопластический материал имеет n = 0. Показатель n не является мерой пластичности металла, обнаружива-емой при разрушении, но чем меньше его значение, тем меньше пластич-ность.

Если известна точка состояния на диаграмме σ_і – _і, то можно определить интенсивность упругих и пластических деформаций, используя соотношения

_iупр = σ _і/3G, (2.36)

где G - модуль сдвига,

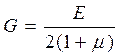. (2.37)

Зная _іпл, можно вычислить составляющие пластических деформа-ций:

_Хпл = 3/2 _іпл/σ_i(σ_х-σ₀); (2.38)

γ_zпл = (3 _іпл/σ_і ) τ_zx. (2.39)

Теория течения

Более точной является теория течения, которая устанавливает еди-ную связь между интенсивностью напряжений σ_i и интегралом ∫ d _iпл

интенсивности увеличений пластических деформаций, независимо от схе-мы напряженного состояния. Величина d _іпл может быть найдена из об-щей зависимости для многоосного нагружения:

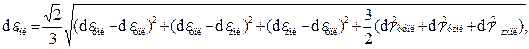(2.40)

где d _хпл, d _yпл…– приращения пластических деформаций на бесконечно малом участке деформирования.

При одноосном растяжении dγ = 0.Тогда с учетом формулы (2.16):

_хпл + _yпл + _zпл = 0; (2.41)

d _yпл = d _zпл = -1/2 d _xпл = -1/2 d _пл.

Из уравнения (2.40) получаем:

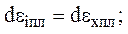(2.42)

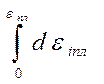= _{хпл= пл}. (2.43)

Плоское напряженное состояние ( σ_z = 0; 0)

Плоская пластина нагружена в ее плоскости (рис.2.13, а). Толщина её δ очень мала по сравнению с размерами а и с. Если выделить элемент с размерами dх, dy и δ в любой точке пластины, то на его гранях возникнут напряжения σ_х, σ_y, τ_xy и τ_yx (рис.2.13, б).

На боковых гранях этого элемента напряжения отсутствуют: σ_z = 0; τ_zx =0; τ_zy = 0, и мы имеем плоское напряженное состояние тела, то есть две параллельных грани бесконечно малого элемента, выделенного в любой точке тела, свободны от напряжений. Напряжения σ_х, σ_y, τ_xy и τ_yx равномерно распределены по толщине пластины.

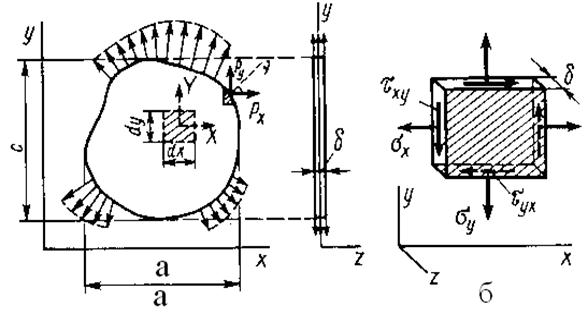
Рисунок 2.13 – Схема определения плоского напряженного состояния

При плоском напряженном состоянии в каждой точке изменяется толщина пластины. Деформация в направлении оси Z по закону Гука равна:

.

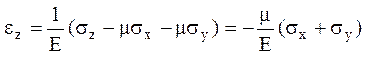Толщина пластины в каждой точке вследствие поперечной деформации изменяется на величину 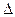δ = _zδ = - 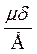(σ_x + σ_y).

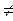Плоская деформация ( _z = 0; σ_z 0)

Имеем очень длинное цилиндрическое тело, равномерно нагружен-ное по всей длине в (рис.2.14, а). Мысленно рассечем это тело на отде-льные слои толщиной δ=1. Если бы эти слои испытывали плоское напря-женное состояние, то в каждой точке пластины толщина изменялась бы на величину Δδ. Но в результате противодействия соседних слоёв это невоз-можно, поэтому каждый слой деформируется в условиях (рис.2.14, б), где он как бы зажат между двумя абсолютно твердыми поверхностями, прину-дительно обеспечивающими условия неизменяемости толщины слоя

Δδ = 0. При этом перемещение во всех точках тела происходит только в параллельных плоскостях XY (см.рис.2.14, б). Так как перемещения W, U, V относительно оси Z отсутствуют, то имеем:

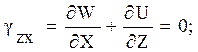
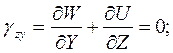
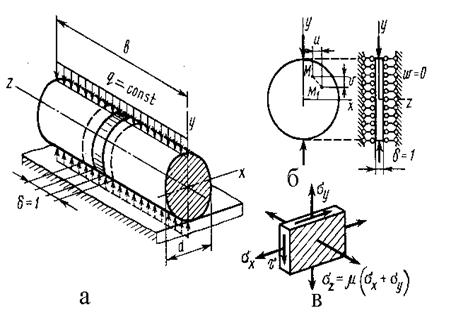
Рисунок 2.14 – Схема определения плоской деформации

Это и есть плоская деформация. По закону Гука имеем:

_z = (σ_z - μσ_x - μσ_y) / E = 0.

В местах, где пластина должна была утолщаться, появятся сжимаю-щие напряжения σ_z, а в местах возможного утонения – растягивающие напряжения σ_z(рис.2.14,в) В обоих случаях

σ_z = μ(σ_x + σ_y). (2.44)

Дата добавления: 2014-11-16