Деформационная теория пластичности

Энергетическая теория пластичности

Теории напряженно-деформированного состояния тела.

По данной теории пластические деформации при объёмно-напряжен-ном состоянии возникают в случае достижения интенсивности напряжений предела текучести:

σ_і = σ_т, (2.23)

где σ_т – предел текучести.

При 3-осном растяжении или сжатии отдельные компоненты могут заметно превосходить σ_т металла, но при этом σ_і < σ_т и пластические деформации не возникнут.

При 2-осном напряженном состоянии, когда σ₁ = -σ₃, а σ₂ = 0, что соответствует чистому сдвигу, пластические деформации начнутся при максимальном напряжении σ_і = σ_т /√3 < σ_т :

σ_і ;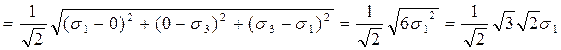

σ_і = _.

Для 1–осного растяжения σ₁ = σ, σ₂ = σ₃ = 0,

.

Для расчетов напряженного состояния за пределами упругих дефор-маций используется деформационная теория пластичности: для различных напряженных состояний металла берется одинаковая экспериментальная зависимость между напряжениями и деформациями. Деформационная тео-рия пластичности устанавливает единую связь между интенсивностью нап-ряжений σ_і и интенсивностью деформаций 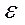_і, независимо от схемы нап-ряженного состояния:

σ_і = ƒ( _і), или σ = Е, (2.24)

где Е – модуль упругости.

Для простого (одноосного) растяжения относительная продольная деформация равняется: 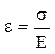, а относительная поперечная деформация .

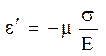Эти два уравнения выражают закон Гука (зависимость между де -формациями и напряжениями) при линейном напряженном состоянии.

Рассмотрим зависимость между деформациями и напряжениями для

объемного напряженного состояния. Возьмем параллелепипед размером

а х b х c ( рис.2.11, а).

Рисунок 2.11 – Вид прямоугольного параллелепипеда (а) и действующих на его гранях напряжений (б)

Из-за деформации рёбра элемента изменят свою длину и станут рав-ными: а + ∆а; b + ∆b; с + ∆с.

Главные относительные удлинения будут равняться:

₁ = ∆а/а; ₂ = ∆b/b; ₃ = ∆с/с,

где ∆а/а, ∆b/b, ∆с/с – относительные удлинения в главных направ-лениях.

₁= ₁΄ + ₁˝ + ₁˝΄,

где ₁΄ – относительное удлинение в направлении σ₁, вызванное действием только напряжения σ₁ (σ₂ = σ₃=0);

₁˝ – относительное удлинение в том же направлении, вызванное действием только напряжения σ₂;

₁˝΄ – относительное удлинение в том же направлении, вызванное действием только напряжения σ_3.

В связи с тем, что направление σ₁ для самого напряжения σ₁ есть продольным, а для напряжений σ₂ и σ₃ – поперечным, находим:

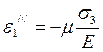
или 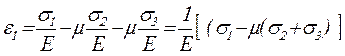. (2.25)

Подобным образом получим формулы и для других главных удлинений:

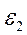
; (2.26)

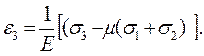(2.27)

Формулы (2.25), (2.26), (2.27) характеризуют обобщенный закон Гука для случая 3-осного напряженного состояния.

Зависимость средней деформации от среднего напряжения имеет вид

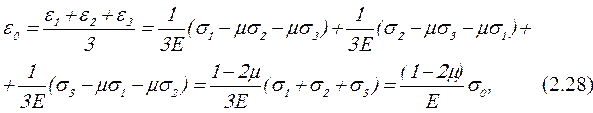
где 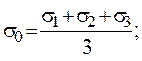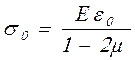; (2.29)

(2.30)

К – объемный модуль упругости,

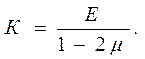(2.31)

При 1 – осном растяжении σ₂ = σ₃ = 0, поэтому σ₀ = σ₁/ 3 = σ/ 3.

Связь между напряжениями и деформациями в любой точке тела

имеет вид:

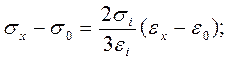
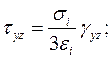(2.32)

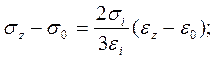
Установим связь между относительным изменением объема _v и главными напряжениями. К началу деформации элемент занимал объем

V_о = а 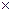в с. В деформированном состоянии его объем определится по уравнению

V= (а + ∆а)(в + ∆в)(с + ∆с) = (а в с)(1+∆а/а)(1+∆b/b)(1+∆с/с) = =V_о(1+ ₁)(1+ ₂)(1+ ₃) = V_о(1+ ₁+ ₂+ ₃ + _{1 2} + _{2 3} +

+ _{3 1}+ _{1 2 3}).

Учитывая маленькое значение относительных линейных деформа-ций, последними четырьмя членами уравнения можно пренебречь. Тогда относительное изменение объема будет иметь вид

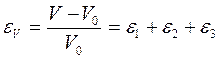. (2.33)

Выразив главные удлинения через главные напряжения в соответ-ствии с формулой (2.28), получим:

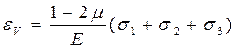. (2.34)

Из формулы (2.34) вытекает, что при деформировании тела, матери-ал которого имеет коэффициент Пуассона μ = 0,5, объем тела не изменя-ется.

Из приведенных выше формул и графической зависимости σ_і от _і (рис.2.12,а) или от ∫ d _iпл (рис.2.12,б) можно по известной деформации вычислить напряжение и, наоборот, по известным напряжениям вычислить деформации.

Для приближенного аналитического описания диаграмм растяжения таких материалов, которые не имеют площадки текучести, и вид диаграмм-мы подобен кривой на рис.2.12,а (высокопрочные стали, аустенитные ста-ли, титановые и алюминиевые сплавы), когда упругой деформацией по сравнению с пластической можно пренебречь, используется зависимость

σ_і = А 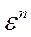_iпл, (2.35)

где А і n - постоянные для конкретного материала.

Дата добавления: 2014-11-16