
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Характеристики сопротивляемости металла разрушению в присутствии концентраторов
|
|
|
|
А б в
А б
Рисунок 3.2 – Касательные силы Р на краю пластины (а) и эпюра
касательных напряжений τ при наличии в зоне текучести металла (б)
При достижении касательными напряжениями предела текучести
τ = τт изменяется форма эпюры τ (рис.3.2, б), изменяется и эпюра σx. При ударном приложении нагрузки σт возрастает, также возрастает и кон-центрация напряжений σx.
С понижением температуры влияние концентрации напряжений на наступление разрушения возрастает по следующей причине. При сниже-нии температуры величина σразр остается почти неизменной, а σт возрас-тает. При одной и той же нагрузке эпюра τ изменяет свой вид (рис. 3.3). Так как возрастает σт, то растёт σxmax в точке 0 при постоянной нагрузке, что приводит к преждевременному разрушению.

Рисунок 3.3 – Распределение касательных напряжений τ при разных
температурах и пределах текучести металла
У высокопрочных материалов величина σт сближается с σ разр, что означает: у основания надреза начало пластической деформации у них соп-ряжено с образованием σxmax, более близких к σразр, чем у сталей обычной прочности, то есть разрушения у высокопрочных сталей при наличии кон-центраторов могут возникнуть при невысоких средних напряжениях.
3.2 Концентрация напряжений и пластические деформации металла при разрушении 
Определение напряженно-деформированного состояния имеет дво-
якое значение: во-первых, знание распределения напряжений и деформа-ций в пределах упругих деформаций позволяет судить о степени напря-женности металла в разных точках детали; во-вторых, без исчерпываю-щего описания напряжений и деформаций при высоких их уровнях невоз-можно определить многие механические характеристики металлов после проведения испытаний образцов, непосредственно связанных с критерия-ми прочности и пластичности. На рис.3.4 приведено распределение напря-жений и размеры зон пластических деформаций в полосе с надрезами.
Одним из проявлений концентрации напряжений является уменьше-ние пластических деформаций металла перед разрушением. Измерение пластических деформаций на полосе с надрезом (см.рис.3.4) показывает, что распределение деформаций очень неравномерное как по поперечному сечению (О-О), так и в направлении действия нагрузки (в сечении А-А). При высокой степени концентрации напряжения к моменту наступления разрушения пластическая деформация может возникнуть лишь вблизи кон- центраторов, в то время как зона I будет оставаться на упругой стадии де-формирования.
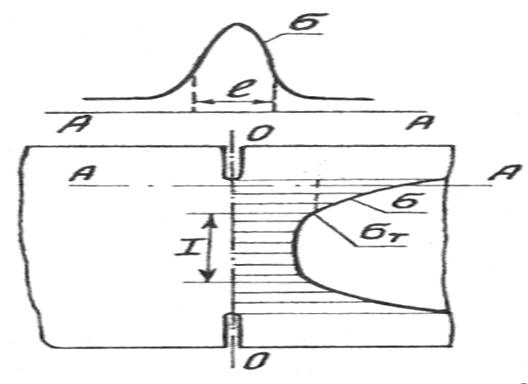
Рисунок 3.4 - Распределение напряжений и размер зоны пластических
деформаций в полосе с надрезами
По сечению А - А пластической деформацией охвачена сравнитель-но небольшая зона размером  . Вот почему концентраторы напряжений являются одной из основных причин появления хрупкости в металлах, ко-торые могут разрушаться после незначительной пластической деформа-ции. Уменьшение объема зон протекания пластической деформации озна- чает уменьшение работы, которую необходимо затратить перед разруше-нием элемента. В экспериментах для этой цели выполняют острые надре- зы на образцах.
. Вот почему концентраторы напряжений являются одной из основных причин появления хрупкости в металлах, ко-торые могут разрушаться после незначительной пластической деформа-ции. Уменьшение объема зон протекания пластической деформации озна- чает уменьшение работы, которую необходимо затратить перед разруше-нием элемента. В экспериментах для этой цели выполняют острые надре- зы на образцах.
Предельно жесткие условия концентрации напряжений наблюдаются при движении трещины в металле. Экспериментальное определение плас- тических деформаций вблизи плоскости разрушения указывает на резкую неравномерность их распределения. Ширина  (рис.3.5) зоны пластичес- ких деформаций различна у разных металлов и может представлять от со-тых до нескольких десятых миллиметра. Величина
(рис.3.5) зоны пластичес- ких деформаций различна у разных металлов и может представлять от со-тых до нескольких десятых миллиметра. Величина 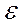 max также разная в зависимости от материала и температуры испытания. Она может изменя-ться у поверхности разрушения от 30...40% до нуля. Пластические дефор-мации еще меньшие, когда при разрушении имеет место плоская деформа-ция, которая в направлении толщины равняется нулю (
max также разная в зависимости от материала и температуры испытания. Она может изменя-ться у поверхности разрушения от 30...40% до нуля. Пластические дефор-мации еще меньшие, когда при разрушении имеет место плоская деформа-ция, которая в направлении толщины равняется нулю (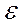 z = 0).
z = 0).

Рисунок 3.5 - Распределение пластических деформаций вблизи поверхности разрушения
Пластины большой толщины, а также хрупкие металлы разрушаются в условиях плоской деформации, протекающей при сохранении неизмен-ности объема металла. Так как при этом утонение металла по толщине не-возможно, то пластическая деформация в вершине трещины возникает преимущественно за счет сдвига металла в крайне ограниченных объемах.
Пластическая деформация сопровождается преобразованием механи- ческой работы в тепло, то есть поглощением энергии. Необходимость зат-рачивать энергию при разрушении, и тем большую, чем больше пластичес-кая деформация металла, является важнейшей особенностью процесса раз-рушения металла.
3.3 Критерии оценки напряженно-деформированного состояния при концентрации напряжений 
При определении механических свойств сварных соединений испо- льзуются стандартные образцы без острых надрезов. Во многих случаях необходимо оценить сопротивляемость металла разрушению на образцах с острыми надрезами. На концентрацию напряжений влияют: форма эле-менмента, его линейные размеры (h, t, в), радиус концентратора ρ, угол между гранями концентратора α (рис.3.6,а) и вид приложенной нагрузки (растяжение, изгиб, сдвиг и т.д.).
σхср = σх в / h.
Рассмотрим тонкую пластину, в которой по толщине σz = 0. В ос-лабленном сечении действуют средние напряжения (рис.3.6, б).
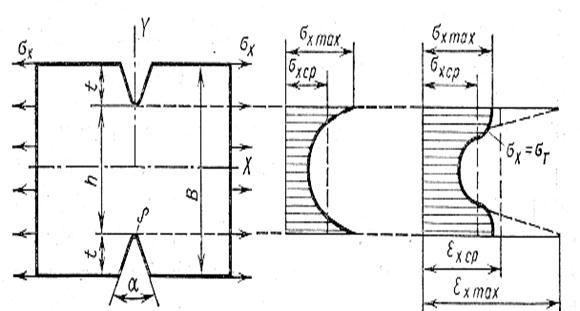
а - общий вид нагруженной пластины;
б - эпюра напряжений в упругом участке;
в - эпюры деформаций и напряжений при σxmax > σт
Рисунок 3.6 - Распределение напряжений и деформаций в пластине
с надрезами
Степень концентрации напряжений при ρ 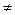 0 принято оценивать ко-эффициентом концентрации напряжений:
0 принято оценивать ко-эффициентом концентрации напряжений:
ασ = σхmax / σхср, (3.2)
где σхmax – максимальное напряжение.
Если пренебречь влиянием напряжений σy в ослабленном сечении, то в упругой области коэффициент концентрации напряжений ασ приблизительно совпадает с коэффициентом концентрации деформаций
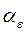 =
= 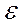 хmax/
хmax/ 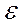 хср. Коэффициенты концентрации ασ и
хср. Коэффициенты концентрации ασ и 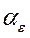 в упругой области не зависят от уровня приложенных напряжений при статической нагрузке.
в упругой области не зависят от уровня приложенных напряжений при статической нагрузке.
Если максимальное напряжение достигает предела текучести σт, то вблизи концентраторов появятся зоны пластических деформаций. Коэффи-циент концентрации напряжений ασ по мере роста нагрузки будет умень-шаться вследствие отставания роста σхmax от σхср (рис.3.6, в).
Если h>>t, то изменение h при t = const мало влияет на коэффициент концентрации напряжений ασ. Такие надрезы называются мелкими. Коэф- фициент концентрации напряжений у них зависит от изменения t. Чем бо- льше t, тем выше коэффициент концентрации напряжений, следовательно,
ασ ≈ √ t. (3.3)
Если t >> h, то коэффициент концентрации напряжений ασ в основ- ном зависит от изменения h и мало зависит от изменения t. Такие надрезы называются глубокими. У них чем больше h, тем выше коэффициент кон-центрации напряжений, то есть.
ασ ≈ √ h. (3.4)
Концентраторы напряжений, характерные для сварных конструкций [8], различаются между собой по следующим признакам: углом α между плоскостями концентратора, радиусом 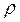 в вершине концентратора, видом напряженного состояния в плоскости АВСД, проходящей через биссектри-су угла α (рис.3.7, а).
в вершине концентратора, видом напряженного состояния в плоскости АВСД, проходящей через биссектри-су угла α (рис.3.7, а).
Напряжение на плоскости АВСД описывается тремя составляющи-ми: нормальными напряжениями σ1 (нормальный отрыв), касательными напряжениями τ2 (сдвиг) и касательными напряжениями τ3 (антиплоский сдвиг), которые являются результатом действия силы Р (рис.3.7, б, в).
В общем случае концентрация напряжений может быть перемен-ной вдоль линии АВ, что определяется характером прикладывания силы Р к частям тела 1 и 2 (см.рис. 3.7,а) и жесткостью самих тел.

 а – форма и схема приложения сил;
а – форма и схема приложения сил;
б, в - характер распределения напряжений
Рисунок 3.7 - Концентратор напряжений в сварном соединении
Если 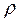 ≠0, то оценку напряженного состояния ведут по коэффици-енту концентрации напряжений ασ или коэффициенту концентрации де-формаций
≠0, то оценку напряженного состояния ведут по коэффици-енту концентрации напряжений ασ или коэффициенту концентрации де-формаций  :
: 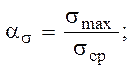
 (3.5)
(3.5)
Чем меньше радиус концентратора 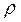 и угол α, тем выше значение коэффициента концентрации напряжений ασ. При α = 0, если грани пара- ллельны, коэффициенты концентрации напряжений определяются выраже-ниями:
и угол α, тем выше значение коэффициента концентрации напряжений ασ. При α = 0, если грани пара- ллельны, коэффициенты концентрации напряжений определяются выраже-ниями:
ασ ≈ √ t / 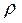 или ασ ≈ √ h /
или ασ ≈ √ h / 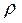 . (3.6)
. (3.6)
Рассмотрим растянутые напряжением σ тонкие бесконечные пласти-ны (плоское напряженное состояние), имеющие вид (рис. 3.8, а, б, в) соот-ветственно: трещины с α = 0 (см.рис. 3.8, а), надрезов (см.рис. 3.8, б) и вы-реза (см.рис.3.8, в).


в
а - трещина с α = 0;
б - размер сечения пластины, в которой расположена
трещина;
в - вырез с α≠ 0
Рисунок 3.8 – Бесконечная пластина с надрезами (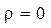 )
)
При  = 0 расчетное напряжение становится равным бесконечнос-ти и понятие коэффициента концентрации напряжений теряет смысл. В ме-ханике разрушения при
= 0 расчетное напряжение становится равным бесконечнос-ти и понятие коэффициента концентрации напряжений теряет смысл. В ме-ханике разрушения при 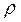 → 0 для оценки напряженно-деформированно-го состояния используют коэффициент интенсивности напряжений в вер-шине трещины при упругих деформациях (К) и понятие коэффициента ин-тенсивности высвобождения энергии деформации (G). Последний крите-рий(в джоулях на квадратный метр) определяется по формуле G= πσ2
→ 0 для оценки напряженно-деформированно-го состояния используют коэффициент интенсивности напряжений в вер-шине трещины при упругих деформациях (К) и понятие коэффициента ин-тенсивности высвобождения энергии деформации (G). Последний крите-рий(в джоулях на квадратный метр) определяется по формуле G= πσ2 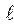 /2Е, означает выделение энергии при подрастании трещины в теле на единицу площади и равен 1-й производной от упругой энергии, накопленной в теле в случае, когда внешние силы не выполняют никакой работы. При этом упругая энергия в теле уменьшается. Если внешние силы одновременно осуществляют работу, то они сообщают телу дополнительную энергию и полная энергия может увеличиваться. Выделенная энергия зависит только от энергии упругой деформации тела и величины подрастания трещины. Работа внешних сил выступает как подведенная к телу энергия, а не как энергия, подводимая к трещине и выделяемая при ее подрастании.
/2Е, означает выделение энергии при подрастании трещины в теле на единицу площади и равен 1-й производной от упругой энергии, накопленной в теле в случае, когда внешние силы не выполняют никакой работы. При этом упругая энергия в теле уменьшается. Если внешние силы одновременно осуществляют работу, то они сообщают телу дополнительную энергию и полная энергия может увеличиваться. Выделенная энергия зависит только от энергии упругой деформации тела и величины подрастания трещины. Работа внешних сил выступает как подведенная к телу энергия, а не как энергия, подводимая к трещине и выделяемая при ее подрастании.
Коэффициент интенсивности напряжений К линейно зависит от при-ложенных по контуру напряжений или сил и пропорционален √ 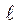 , где
, где 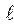 - длина трещины (см.рис.3.8, а), размер опасного сечения образца (см.рис.3.8, б) или выреза (см.рис.3.8, в), равен МПа·м ½:
- длина трещины (см.рис.3.8, а), размер опасного сечения образца (см.рис.3.8, б) или выреза (см.рис.3.8, в), равен МПа·м ½:
К = √π/2  σ√
σ√  , (3.7)
, (3.7)
где σ - среднее напряжение в ослабленном или в неослабленном се-чении на некотором расстоянии от трещины.
Между коэффициентами К и G существуют зависимости:
G = K2/E – для плоского напряженного состояния; (3.8)
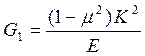 – для плоского деформированного состояния. (3.9)
– для плоского деформированного состояния. (3.9)
Величины К и G используются для оценки свойств металла при нали-чии в нём трещины.
Чувствительность металла к концентрации напряжений в случае кон-центраторов с надрезами может также оцениваться величиной коэффици-ента концентрации αт, при котором широкий образец со щелевидным над-резом разрушается при напряжении, равном пределу текучести σт , опреде-ляется по формуле Нойбера:
αт = Ö ασ 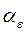 , (3.10)
, (3.10)
где ασ и 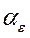 - коэффициенты концентрации, соответственно, напря-жений и деформаций.
- коэффициенты концентрации, соответственно, напря-жений и деформаций.
В момент наступления разрушения в концентраторе достигается ис -тинное разрушающее напряжение σразр и разрушающая деформация 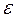 разр, которые могут быть определены при одноосевом растяжении гладкого об-разца. Средние напряжения и деформации, соответственно, равны σт и
разр, которые могут быть определены при одноосевом растяжении гладкого об-разца. Средние напряжения и деформации, соответственно, равны σт и  т = σт / Е; тогда
т = σт / Е; тогда 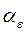 =
= 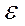 разр/
разр/ 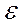 т и ασ = σ разр / σт. Подставляя эти значения в формулу Нойбера, получим:
т и ασ = σ разр / σт. Подставляя эти значения в формулу Нойбера, получим:

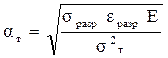 . (3.11)
. (3.11)
В качестве характеристики напряженно-деформированного состоя-ния используют также понятие раскрытия вершины концентратора δ. Пер-воначально оно применялось к концентраторам с ρ ≠ 0 и означало увели-чение а в основании выреза (рис.3.9, а), определяемое как разность А1В1 после нагружения и АВ-до нагружения:
δ = А1В1 – АВ. (3.12)

а - изменение расстояния между точками А и В;
б - раскрытие конца трещины;
в - интеграл упругопластических деформаций
Рисунок 3.9 - Разные случаи определения величины
раскрытия вершины трещины
Затем это понятие было перенесено на трещины (рис.3.9,б), но при этом довольно сложно точно определить величину раскрытия трещины. В настоящее время за критерий δ используется интеграл упругопластичес-ких деформаций  на длине СD (рис.3.9, в).
на длине СD (рис.3.9, в).
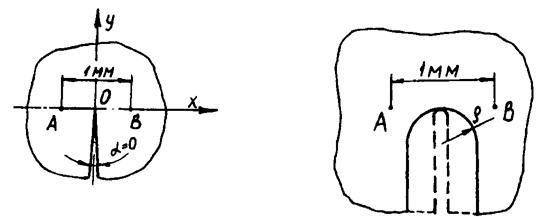
В сварных соединениях существует непрерывный спектр изменения ρ от нуля до долей миллиметра и более (стыковые и тавровые соединения, несплавление, переход от шва к основному металлу) в зависимости от по-верхностного натяжения у жидкого металла и условий его деформирова-ния. При ρ < 0,5 мм условная база перемещения может быть взята равной 1мм (рис.3.10), а вместо реального предела тела, показанного сплошной линией, можно принимать предел, показанный штриховой линией (рис.3.10,б).
К деформационным критериям относится также критерий динами-ческого раскрытия трещины  при ее быстром распространении в ус-ловиях плоского напряженного состояния. В листовых металлах зона пла-стической деформации при разрушении значительно больше толщины ме-талла.
при ее быстром распространении в ус-ловиях плоского напряженного состояния. В листовых металлах зона пла-стической деформации при разрушении значительно больше толщины ме-талла.
а– 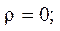 б–
б– 
Рисунок 3.10 - Схема расположения базы 1мм у острия надреза
при  и разных значениях
и разных значениях 
По существу применительно к листовым металлам деформационный критерий раскрытия трещины представляет интеграл поперечных пласти-ческих деформаций  упл, возникающих в процессе распространения тре-щины слева и справа от нее (рис. 3.11).
упл, возникающих в процессе распространения тре-щины слева и справа от нее (рис. 3.11).

где 2bпл – размер ширины зоны пластических деформаций.


Рисунок 3.11 - Схема продольных (а) и поперечных (б) пластических
деформаций возле края разрыва
Для случаев деформированного состояния металла вблизи острых надрезов и трещин за пределами упругости используется коэффициент ин-тенсивности деформаций V, м 1/2, который в простом случае концентра-тора с параллельными гранями при α = 0 вычисляется по формуле
V =  max
max 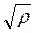 =
=  ср.
ср. 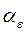
 . (3.13)
. (3.13)
Комплекс 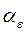
 слабо зависит от ρ, так как в случае параллель-ных граней надреза коэффициент концентрации ασ ≈ А/
слабо зависит от ρ, так как в случае параллель-ных граней надреза коэффициент концентрации ασ ≈ А/  . Значение ве-личины А пропорционально √
. Значение ве-личины А пропорционально √  . При ρ = 0 (трещина) значение величи-ны V с точностью до постоянного коэффициента совпадает с коэффи-циентом интенсивности напряжений К. В упругой области между V и К имеется связь:
. При ρ = 0 (трещина) значение величи-ны V с точностью до постоянного коэффициента совпадает с коэффи-циентом интенсивности напряжений К. В упругой области между V и К имеется связь:
V = 2К/(√π Е). (3.14)
При α ≠ 0 величины V и К зависят от угла α. Таким образом, для численного определения V по формуле (3.14) необходимо знать геометри-ческие размеры тела и среднюю деформацию 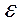 ср.
ср.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 762; Нарушение авторских прав?; Мы поможем в написании вашей работы!