Область устойчивости САУ

Для анализа и синтеза САУ необходимо провести исследование влияния ее параметров на устойчивость. При решении этой задачи применяют понятие области устойчивости, которая зависит от диапазона изменений величин параметров, при которых САУ устойчива. Область устойчивости чаще всего строят в плоскости двух параметров. В связи со сложностью графического представления поверхностей (границ) области устойчивости в трехмерном изображении, построение области устойчивости, в зависимости от трех параметров, применяется редко. Например, выше было рассмотрено условие устойчивости, при котором корни характеристического уравнения системы должны находиться в отрицательной полуплоскости комплексной плоскости. В этом случае областью устойчивости считается левая (отрицательная) полуплоскость.

Для определения области устойчивости необходимо построить границы устойчивости первого (при нулевом корне характеристического уравнения) и второго (при наличии только мнимых корней) типов. Чаще всего достаточно построить только границы устойчивости второго типа (колебательной границы устойчивости). Для ее расчета можно пользоваться различными критериями устойчивости.

Для определения области устойчивости САУ, описываемой уравнениями не выше пятого порядка (при n ≤ 5), возможно применение критерия Гурвица.

Система будет находиться на колебательной границе устойчивости в том случае, когда предпоследний определитель Гурвица равен нулю (D_n-1 = 0).

Критерий Михайлова может использоваться независимо от порядка уравнения. Система будет находиться на границе устойчивости в том случае, когда будут выполняться следующие условия:

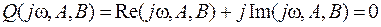(2.53.)

В данном выражении A, B являются параметрами САУ, наиболее влияющими на ее устойчивость. Условие нахождения САУ на границе устойчивости (2.53.) можно представить, как систему из двух условий:

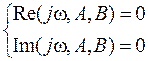(2.54.)

Уравнения системы будут представлены параметрическими уравнениями колебательной границы устойчивости в плоскости с координатами А и В при условии, что действительные части всех других корней будут отрицательными, кроме чисто мнимых корней. Любой точке, находящейся на границе устойчивости, будет соответствовать значение чисто мнимого корня, а значит, будет соответствовать частота колебаний величины выходного параметра. Пример границы области устойчивости ПИ-регулятора в зависимости от величины его параметров (передаточного коэффициента k _p и постоянной интегрирования T_и) изображен на рисунке 76.

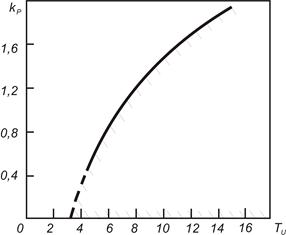
Рис.76. Граница и область устойчивости ПИ-регулятора

Областью устойчивости будет являться часть квадранта ниже кривой и выше оси T_и, штриховка указывает направление расположения области. Границей устойчивости первого типа будет являться ось T_и, где k_р= 0, т.к. в этом случае характеристическое

уравнение замкнутой системы будет иметь нулевой корень.

Дата добавления: 2014-11-16