Поняття про ряди розподілу, їх види

РЯДИ РОЗПОДІЛУ. АНАЛІЗ ВАРІАЦІЇ ТА ФОРМИ РОЗПОДІЛУ

Розділ 6

Задачі для самостійного розв’язання

5.1. Розрахувати середню заробітну плату персоналу в лінійному цеху МТС у базовому і звітному періодах. Якщо середня заробітна плата персоналу відрізняється, пояснити чому.

Таблиця 5.9 – Динаміка заробітної плати і персоналу в лінійному цеху МТС

Посада	Чисельність робітників, чол.	Зарплата в місяць, грн.	Чисельність робітників, чол.	Зарплата в місяць, грн.
Інженер
Старший технік
Технік
Монтер
Разом		–		–

5.2. Виконання плану виробництва продукції характеризується даними на п'яти підприємствах галузі (табл. 5.10). Визначити середній відсоток виконання плану в цілому по підприємствах. Зробити висновки.

Таблиця 5.10 – Виробництво продукції на п'яти підприємствах галузі

№ підприємства	Вироблено продукції, тис. грн.	Вироблено продукції, % до плану
	19,1	94,7
	11,5	101,4
	25,7	100,2
	8,3	93,5
	9,7	102,0

5.3. Розрахувати середньодобове надходження повідомлень електронної пошти за наступними даними (табл. 5.11).

Таблиця 5.11 – Добове надходження електронних повідомлень організації

зв'язку

Кількість повідомлень на добу, шт.	Кількість діб
1000 – 1100
1100 – 1200
1200 – 1300
1300 – 1400
1400 – 1500
1500 – 1600
Разом:

5.4. Розрахувати середню тривалість заняття телефонної лінії ММТС на добу.

Таблиця 5.12 – Тривалість заняття телефонної лінії ММТС

Тривалість телефонних з'єднань, хв.	Частка населення, %
До 10	2,1
10 – 20	5,6
20 – 30	11,8
30 – 40	19,1
40 – 50	17,4
50 – 60	12,5
60 – 70	3,6
70 – 80	2,7
80 – 90	3,3
90 – 100	3,0
100 – 110	3,7
110 – 120	2,1
120 – 130	1,8
130 – 140	2,2
140 – 150	3,8
Більше 150	5,3
Разом:	100,0

5.5. Потрібно розрахувати середній курс продажу акцій телекомунікаційної компанії по даним про середній курс продажу акцій за трьома операціями на фондовій біржі і вартості проданих у результаті цих операцій акцій.

Таблиця 5.13 – Середній курс продажу акцій та вартість проданих акцій

Номери операцій	Середній курс продажу акцій, тис. грн.	Вартість проданих акцій, тис. грн.
I	1,36	27,2
II	1,48	44,4
III	1,57	31,4
Разом:	×	103,0

5.6. Потрібно установити, чи виконується контрольний термін установлення пошкоджень групового обладнання АТС (контрольний термін складає 45 хв.) бригадою монтерів. Один монтер на установлення пошкодження витрачає 40 хв., другий – 45 хв., а третій – 50 хв. Знайти середній час усунення пошкодження в бригаді, якщо відомо, що перший монтер працював 6,0 год.; другий, – 1,5 год.; третій, – 2,5 год.

5.7. За даними табл. 5.14 визначити середньорічний темп зростання споживчих цін 2005 – 2008 рр.

Таблиця 5.14 – Індекси споживчих цін у % до попереднього року

Рік
Темп зростання	101,7	121,0	97,2	105,0

План

6.1. Поняття про ряди розподілу, їх види.

6.2. Поняття про показники варіації і способи їх обчислення.

6.3. Види дисперсій і правило їх додавання.

6.4. Форми рядів розподілу та їх характеристика.

6.5. Графічне зображення рядів розподілу.

В результаті статистичного групування отримують ряди цифрових показників, які характеризують розподіл одиниць досліджуваної сукупності за варіаційною ознакою. Такі ряди називаються рядами розподілу.

Ряд розподілу складається з двох елементів – варіантів та частот.

Варіанти (х) – це окремі значення групувальної ознаки, які розташовані в певній послідовності.

Частоти (f) – це числа, які показують, скільки разів певне значення ознаки зустрічається у сукупності, або скільки одиниць сукупності припадає на кожну групу.

Ряди розподілу відіграють важливу роль при вивченні складу сукупності за досліджуваною ознакою, закономірностей розподілу, використовуються при визначенні середніх величин, показників варіації, взаємозв’язку та ін.

В залежності від характеру групувальної ознаки ряди розподілу поділяються на атрибутивні та варіаційні (кількісні).

В атрибутивних рядах розподілу варіанти не мають числового виразу.

Варіаційні ряди, в яких варіанти мають числовий вираз, поділяються на дискретні та інтервальні. В дискретних рядах варіанти являють собою дискретні числа, в інтервальних – це інтервали групування.

У тому випадку, коли виконуються групування за двома і більше ознаками отримують комбінаційний ряд розподілу.

При побудові атрибутивних рядів розподілу варіанти потрібно розташувати в логічній послідовності. При використанні дискретних та інтервальних варіаційних рядів варіанти записують в порядку зростання. Для інтервальних рядів важливим є чітке розмежування варіант.

Розрізняють ряди розподілу з абсолютними, відносними та нагромадже­ними частотами. Нагромаджені частоти ще називають кумулятивними. В пер­шому випадку чистоти являють собою абсолютні числа, в другому – питому вагу або частку кожної групи.

Ряди розподілу з абсолютними частотами характеризують склад сукупності, а з відносними – структуру сукупності.

Ряди розподілу з нагромадженими (кумулятивними) частотами пока­зують, яка чисельність або питома вага одиниць має значення ознаки менше за дане. Кумулятивні частоти знаходять шляхом їх сумування за групами.

Щільність розподілу – це кількість одиниць сукупності, що припадає на одиницю величини інтервалу групувальної ознаки. Розрізняють абсолютну щільність і відносну:

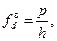
де f – частота;

р – частка (доля); h – величина (розмір) інтервалу.

Приклад. Маємо наступні дані про розподіл сімей за місячним доходом:

Таблиця 6.1 – Розподіл сімей за місячним доходом

Місячний доход на одного члена сім’ї, грн.	Число сімей	Щільнісь розпроділу
одиниць	%	число сімей	%
До 200,0		13,2	0,17	0,066
200,0 – 400,0		20,2	0,26	0,101
400,0 – 600,0		27,9	0,36	0,140
600,0 – 1000,0		27,1	0,18	0,068
1000,0 – 1500,0		11,6	0,06	0,023
Разом:		100,0	×	×

Отже, найбільшу щільність розподілу має третя група сімей з доходом 400,0 –600,0 грн. на одного члена сім'ї.

Інтерполяція в рядах розподілу визначає, скільки одиниць сукупності (абовідсотків) мають значення ознаки менше за задане. Для інтерполяціївикористовують як абсолютні, так і відносні нагромаджені частоти.

Приклад. Маємо наступні дані про розподіл сімей за місячним доходом:

Таблиця 6.2 – Розподіл сімей за місячним доходом

Місячний доход на одного члена сім’ї, грн.	Нагромаджені частоти
Число сімей	%
До 200,0		13,0
200,0 – 400,0		33,4
400,0 – 600,0		61,3
600,0 – 1000,0		88,4
1000,0 – 1500,0		100,0

Визначити:

а) скільки сімей мають доход менше 5000 грн. на одного члена сім'ї.

Розрахунок:

f_x < 5000 = 86 + 0,5(158 – 86) = 122 сім'ї,

або

f_x < 5000 = 33,4 + 0,5(61,3 – 33,4) = 47,4 %.

Таким чином, 122 (47,4 %) сімей мають доход менше 5000 грн. на одного члена сім'ї.

б) скільки сімей мають доход менше 7300 грн. на одного члена сім'ї.

Розрахунок:

сімей.

Таким чином, 181 (70,1 %) сімей мають доход менше 7300 грн. на одного члена сім'ї.

Дата добавления: 2014-11-08