Види дисперсій і правило їх додавання

Для більш детального вивчення тієї або іншої ознаки, статистика за допомогою правила додавання дисперсій виявляє і досліджує вплив окремих факторів і умов, які зумовили дану варіацію в цілому. Виявити частку варіації, зумовлену певними факторами, можна поділивши всю сукупність на групи за ознакою, вплив якої досліджується.

Якщо сукупність поділена на групи за одним фактором, то для неї можна обчислити такі види дисперсій: загальну, групову (часткову), середню з групових і міжгрупову.

Загальна дисперсія вивчається як середня арифметична з квадратів відхилень кожного значення ознаки від їх загальної середньої величини. Дана дисперсія характеризує варіацію досліджуваної ознаки за рахунок впливу всіх факторів. Її розраховують за формулами:

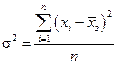– проста; 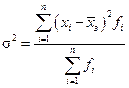– зважена.

Групова (часткова) дисперсія визначається як середня арифметична з квадратів відхилень кожного значення ознаки в групі від групової середньої. Групові дисперсії визначаються за формулами:

проста; 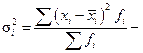зважена,

де 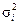– групова (часткова) дисперсія;

х_і – індивідуальні значення групових ознак;

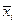– середнє значення ознак і- їгрупи;

п – число одиниць сукупності в групі;

f_i – частоти в групі.

Групова (часткова) дисперсія вимірює варіацію ознаки тільки за рахунок факторів, які діють усередині групи, тобто всіх факторів, крім покладеного в основу групування.

Середню з групових (залишкову) дисперсію визначають за формулами середньої арифметичної із групових дисперсій:

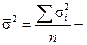проста; 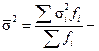зважена.

Міжгрупова дисперсія визначається як середня арифметична з квадратів відхилень групових середніх від загальної середньої за формулами:

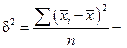проста; 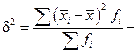зважена,

де 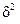– міжгрупова дисперсія;

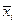– групові середні;

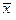– загальна середня;

п – число одиниць сукупності;

f_i – ваги або частоти.

Міжгрупова дисперсія відображає варіацію досліджуваної ознаки під впливом фактора, покладеного в основу групування.

Математичною статистикою доведено, що між загальною дисперсією, середньою з групових дисперсій і міжгруповою дисперсіями існує зв'язок:

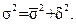
Ця рівність у статистиці називається правилом додавання дисперсій. За допомогою даного правила, знаючи два види дисперсій, завжди можна визначити невідомий третій вид:

; .

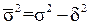Правило додавання дисперсій використовують при проведенні вибіркового спостереження, для спрощеного обчислення дисперсій громіздкого варіаційного ряду, вимірювання тісноти зв’язку між явищами та ін.

Проілюструємо застосування правила додавання дисперсій на прикладі.

Приклад. Нехай маємо відомості про годинну заробітну плату десяти працівників, поділених на дві групи за рівнем фахової підготовки.

Таблиця 6.6 – Розрахункова таблиця

Перша група	Друга група
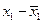
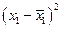
Табельний номер працівника, (п 1)	Годинна заробітна плата працівників-практиків, грн. (х 1)			Табельний номер працівника, (п 2)	Годинна заробітна плата працівників з ПТУ, грн. (х 2 )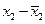
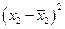
	6,0 6,3 6,5 6,8 7,0	-0,52 -0,22 -0,02 0,28 0,48	0,2704 0,0484 0,0004 0,0784 0,2304		8,2 8,5 8,6 8,8 9,0	-0,42 -0,12 -0,02 0,18 0,38	0,1764 0,0144 0,0004 0,0324 0,1444
Разом:	32,6	×	0,6280	Разом:	43,1	×	0,3680

Обчислимо середньогодинну заробітну плату працівників для кожної групи:

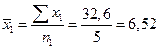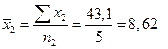грн.; грн.

За даними розрахункової таблиці визначимо групові дисперсії:

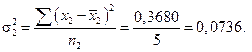
Середня з групових дисперсій дорівнює:

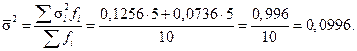
Для знаходження міжгрупової дисперсії потрібно обчислити загальну середню годинну заробітну плату всіх працівників за формулою середньої арифметично зваженої з групових середніх:

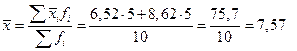грн.,

або за формулою середньої арифметичної простої:

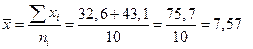грн.

Обчислимо міжгрупову дисперсію:

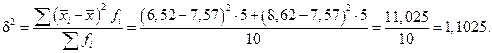
Використавши правило додавання дисперсій, визначимо загальну дисперсію:

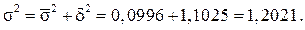
Правильність наших розрахунків можна перевірити, обчисливши загальну дисперсію звичайним способом:

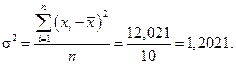
Як показала перевірка, результати обчислення загальної дисперсії за обо­ма способами такі ж самі, що свідчить про правильність проведених розрахунків.

Середнє квадратичне відхилення із загальної дисперсії дорівнює:

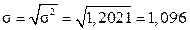грн.

Таким чином ми визначили, що середня годинна заробітна плата групи працівників у кількості десяти чоловік склала 7,57 грн., за середнього квадратичного відхилення 1,096 грн.

При цьому можемо стверджувати, що якщо загальна дисперсія склала 1,2021, то міжгрупова дисперсія в розмірі 1,1025 викликана різницями кваліфікації в групах працівників, а середня з групових дисперсій в розмірі 0,0996 показує частку впливу усіх, крім покладеного в основу групування, факторів. Правило додавання дисперсій дозволяє визначити частку складових частин у загальній дисперсії.

Поділивши міжгрупову дисперсію на загальну дисперсію отримаємо показник, який називається коефіцієнтом детермінації 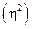і показує, яка частка всієї варіації ознаки, зумовлена ознакою, покладеною в основу групування. В даному прикладі:

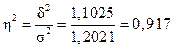або91,7 %,

де 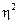–(грецька буква «ета» в квадраті) – коефіцієнт детермінації.

Отже, фактор кваліфікації робітників на 91,7 % зумовлює варіацію їхньої середньогодинної заробітної плати.

Корінь квадратний з коефіцієнта детермінації називають емпіричним кореляційним відношенням, яке показує тісноту (силу) зв’язку між групувальною та результативною ознаками.

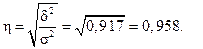
Це говорить про те, що зв'язок між кваліфікацією працівників та їхньою середньогодинною заробітною платою надто сильний (тісний).

Спрощені способи розрахунку дисперсії. Обчислення дисперсії і середнього квадратичного відхилення пов’язане з великими і складними розрахунками, які потребують значних затрат часу і праці. Проте їх можна значно спростити, якщо використати деякі математичні властивості дисперсії.

1. Якщо всі варіанти ознаки (x) зменшити на довільну величину (А), то дисперсія від цього не зміниться.

2. Якщо всі значення варіантів (x) зменшити в (A) разів, то дисперсія зменшиться в (A ²) разів, а середнє квадратичне відхилення – в (A) разів.

3. Якщо обчислити середній квадрат відхилень від будь-якої величини А, яка тою або іншою мірою відрізняється від середньої арифметичної (x), то він завжди буде більший за середній квадрат відхилень, обчислений від середньої арифметичної, на квадрат різниці між середньою і цією умовно взятою величиною, тобто на (x – А)².

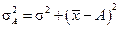або ,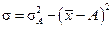

де 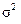– середній квадрат відхилень від середньої арифметичної ;

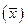– середній квадрат відхилень від довільної величини (А).

Дата добавления: 2014-11-08