I уровень

ПО МОДУЛЮ

МАТЕРИАЛЫ К ЛАБОРАТОРНОЙ РАБОТЕ

Тема: Алгоритмы разветвляющейся структуры.

Цель: уметь составлять схемы алгоритмов разветвляющейся структуры и программы на языке Turbo-Pascal для решения практических задач.

Студенту следует для трех задач, условия которых приведены ниже, выполнить следующие задания:

· составить схему алгоритма решения задачи;

· записать пояснения к схеме алгоритма;

· составить программу на языке Turbo-Pascal;

· проверить выполнение составленной программы на контрольном примере, приняв упрощенные значения исходных данных по своему усмотрению.

Наиболее наглядным способом составления алгоритма является графический, т. е. изображение алгоритма решения задачи в виде схемы. При составлении алгоритмов разветвляющейся структуры необходимо указать дальнейшее направление вычислительного процесса по одному из нескольких заранее определенных направлений в зависимости от выполнения некоторого логического условия.

При составлении схем алгоритма следует:

· четко определить, что является исходными данными и в каком виде должен получиться результат решения задачи;

· словесно сформулировать действия, которые необходимо выполнить для получения результата решения задачи, затем записать последовательность действий с помощью блоков в виде схемы алгоритма.

ПРИМЕРЫ РАЗНОУРОВНЕВЫХ ЗАДАНИЙ
ДЛЯ КОНТРОЛЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ

Вариант 1

1. Вычислить R при любых заданных значениях x и а:

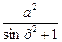, если х < 0;

R =

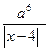, если х ³ 0.

2. Даны три числа a, b, c. Напечатать те из них, которые меньше 15.

3.Взвешивание поросенка показало, что его масса за n дней увеличилась с m1 до m2 кг. Определить, достигнет ли среднесуточный привес поросенка запланированной нормы d кг.

Вариант 2

1. Вычислить Z при любых заданных значениях a, b, t:

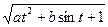, при t < 0,1

Z = at + b, при t = 0,1

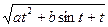, при t > 0,1

2. Даны три числа a, b, c. Напечатать те из них, которые больше 0, но меньше 10.

3. Вывести на экран номера точек с координатами А(x ₁, y ₁), В(x ₂, y ₂), С(x ₃, y ₃), которые лежат на оси ОХ, и определить их количество.

Вариант 3

1. Вычислить S при любых заданных значениях a, b, c, f:

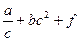, при c < 3;

S = c – cos f, при 3 £ c £ 7;

ac + bc ³, при c > 7.

2. Даны две фигуры: квадрат со стороной a и круг с радиусом r. Определить, какая из фигур имеет бόльшую площадь, и вывести эту площадь на печать.

3. Определить, попадет ли команда “Динамо” в лигу сильнейших (т. е. наберет не менее 20 очков). За выигрыш команда получает 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. Команда m встреч выиграла, k – проиграла, а p завершила вничью.

Вариант 4

1. Вычислить D при любых заданных значениях a, c, x:

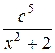, если х < 0;

D =

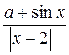, если х ³ 0.

2. Даны три числа a, b, c. Напечатать те из них, которые больше заданной величины z. Если таких чисел нет – вывести сообщение об этом.

3. Определить, можно ли огородить изгородью длиной z два земельных участка, имеющих форму прямоугольника со сторонами c, d и форму квадрата со стороной a.

Вариант 5

1. Вычислить Z при любых заданных значениях a, b, t:

t ² + 2 a – b, при t < 0,1;

Z = at + b, при t = 0,1;

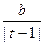, при t > 0,1.

2. Даны три неравных между собой числа a, b, c. Наибольшее из них разделить на сумму двух оставшихся. Вывести на экран полученный результат и наибольшее число.

3. Определить и вывести на экран номера точек с координатами А(x ₁, y ₁), В(x ₂, y ₂), С(x ₃, y ₃), которые лежат на оси ОY.

Дата добавления: 2014-11-08