III уровень

Вариант 25

1. Вычислить U при любых заданных значениях x, a, b:

x ² – 3 a + cos² x, при х £ 3;

U = | b – a |, при 3 < x £ 5;

(x ³ – 4), при x >5.

2. Определить, является ли треугольник со сторонами a, b, c прямоугольным (для определения использовать теорему Пифагора).

3. Определить, какая из трех точек с координатами А(x ₁, y ₁), В(x ₂, y ₂), С(x ₃, y ₃) лежит ближе к началу координат и вывести на печать ее номер.

Вариант 26

1. Вычислить F для любых произвольных значений х и с:

F =

2. Задана окружность с центром в начале координат и точка А с координатами (x, y), лежащая на окружности. Определить, можно ли в этот круг вписать квадрат со стороной d.

3. Надои молока, полученные каждой из трех доярок Петровой, Ивановой, Сидоровой за 30 дней, составляют соответственно Р1, Р2, Р3 литров. Вывести на печать фамилии и надои тех доярок, среднесуточные надои которых достигают планового показателя, равного R литров.

Вариант 27

1. Вычислить R при любых заданных значениях x, a, b:

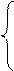
, если x < a;

R = x – a + b, если x = а;

ba – cos² x, если x > a.

2. Бригада из четырех рабочих собирала картофель, каждый собрал соответственно a, b, c, d ( кг ). Определить, превышает ли средняя выработка в бригаде заданную величину S ( кг ) и вывести на печать номера рабочих, которые не достигли средней выработки по бригаде.

3. Даны три неравных между собой числа x, y, z. Наибольшее из них разделить на сумму двух других.

Вариант 28

1. Вычислить D для любых произвольных значений х и с:

D =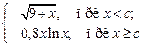

2. Определить, поместится ли круг с радиусом r вквадрат со стороной a.

3. Три студента сдали три экзамена и получили соответственно оценки: I студент – x1, x2, x3; II студент – y1, y2, y3; III студент – z1, z2, z3. Вывести на печать номера тех студентов, которые будут получать стипендию, если для этого необходимо иметь средний балл, равный 7,5.

Вариант 29

1. Вычислить G для любых произвольных значений х и с:

G =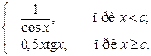

2. Вычислить Q = max (x, y, z) + 4. Значение x, y, z заданы.

3. Заданы три точки с координатами А(x ₁, y ₁), В(x ₂, y ₂), С(x ₃, y ₃) и круг c центром в начале координат и радиусом R. Определить, сколько точек принадлежит кругу.

Вариант 30

1. Вычислить B для любых произвольных значений х и с:

B =

2. Вычислить Q = min (x, y, z) + d. Значение x, y, z, d заданы.

3. Цех по переработке молочной продукции за одну смену выпускает пастеризованного молока a кг, кефира – b кг. Определить, выполнит ли цех плановые показатели за месяц (30 дней) по каждому из видов продукции, составляющих соответственно s кг и p кг, если в первую декаду он работал в одну смену, во вторую – в полторы, в третью – в две смены.

ЗАДАНИЯ ДЛЯ УПРАВЛЯЕМОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ

Самостоятельно изучить и выполнить раздел дисциплины «Программирование алгоритмов линейной структуры» по плану:

1) составить схемы алгоритмов решения задач (используя графический способ описания алгоритма): детальную и укрупненную. Записать пояснения к схемам алгоритмов;

2) составить программы на языке Turbo-Pascal;

3) проверить выполнение составленных программ на конкретном примере, приняв упрощенные значения исходных данных по своему усмотрению.

Вариант 1

1. Составить схему алгоритма и программу для вычисления выражения:

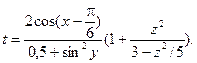
2. Садовый участок имеет форму полукруга, диаметр которого равен D (м). Участок по всему периметру необходимо огородить забором. Определить, какое количество столбиков и сколько рулонов сетки необходимо заказать для забора, если расстояние между столбиками должно быть Z (м), а длина одного рулона сетки – G (м). В программе результаты расчета округлить до ближайшего целого числа в большую сторону.

Вариант 2

1. Составить схему алгоритма и программу для вычисления выражения:

.

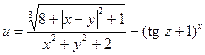2. Картофельное поле имеет форму треугольника со сторонами А (м), В (м) и С (м). На ручной уборке картофеля задействована группа из N студентов, причем ребята составляют М % от общего числа студентов, остальной состав группы – девушки. Скорость уборки картофеля ребятами за 1 час работы составляет R (м²), а девушками – D (м²). Сколько дней необходимо запланировать на уборку поля, если продолжительность рабочего дня составляет Т часов, из которых Р часов используется на обеденный перерыв. В программе результат расчета округлить до ближайшего целого числа в большую сторону.

Вариант 3

1. Составить схему алгоритма и программу для вычисления выражения:

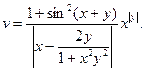
2. Длина, ширина и высота дома – А, В и Н (м) соответственно. Дом имеет крышу, которая в поперечном сечении образует над потолком равнобедренный треугольник высотой V (м). Поверхность в торце дома, заключенная между крышей и потолком, называется фронтоном. В доме имеется одна дверь размером С × D (м) и N окон размером Е × F (м). Стены дома планируется окрасить в зеленый цвет, фронтоны – в желтый, а крышу – в коричневый. Окна и двери решено не перекрашивать. Определить необходимое количество краски каждого цвета (в кг). Расход краски составляет Q (грамм на 1 м²).

Вариант 4

1. Составить схему алгоритма и программу для вычисления выражения

.

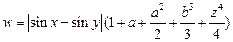2. Автохозяйство имеет N легковых и М грузовых автомобилей. Плановый пробег за месяц эксплуатации одного легкового автомобиля составляет L 1 (км), а грузового – L 2 (км). Норма расхода бензина для легковых автомобилей составляет Q 1 (литров на 100 км), а для грузовых – Q 2 (литров на 100 км). Определить общую годовую потребность автохозяйства в бензине (в литрах), если фактически легковые автомобили простаивают без пробега Р 1 % времени в году, а грузовые – Р 2 %.

Вариант 5

1. Составить схему алгоритма и программу для вычисления выражения:

.

2. Фермер имеет в своем хозяйстве N коров и М телят. Суточное потребление сена на одну корову составляет Q 1 (кг), на одного теленка – Q 2 (кг). На зиму фермер заготовил К 1 тюков сена цилиндрической формы диаметром D (м) и высотой Н (м) и К 2 тюков сена в форме параллелепипеда размером А × В × С (м). Удельный вес сена в тюках составляет R (кг/м³). Рассчитать количество дней, в течение которых фермер сможет прокормить животных. В программе предусмотреть округление результата до ближайшего меньшего целого числа.

Вариант 6

1. Составить схему алгоритма и программу для вычисления выражения:

.

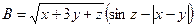2. На уборке зерновых задействовано два комбайна, имеющие производительность работы Q 1 и Q 2 (га/час), которые вместе должны убрать площадь S (га). Первый комбайн убирает К % всей площади, остальное – второй комбайн. Часовой расход топлива при работе комбайнов составляет R 1 и R 2 (л/ час) соответственно. Определить, сколько тонн топлива потребуется для уборки урожая, если удельный вес топлива составляет Р (кг/л), и затраты хозяйства на топливо, если стоимость 1 тонны топлива составляет С (руб.).

Вариант 7

1. Составить схему алгоритма и программу для вычисления выражения:

.

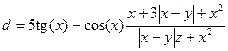2. Рожью засеяна площадь S 1 (га), пшеницей – S 2 (га). Урожайность ржи составляет Q 1 (ц/га), пшеницы – Q 2 (ц/га). Для доставки зерна с поля на элеватор используются автомобили грузоподъемностью Р тонн. Продолжительность рабочего дня составляет Т часов, на выполнение одного рейса (с поля на элеватор и обратно) автомобилю требуется R часов. Определить, сколько автомобилей необходимо привлечь к работе, чтобы обеспечить доставку зерна с поля за N дней. Указание: при расчете числа рейсов, которые выполняет один автомобиль за день, в программе предусмотреть округление результата до ближайшего меньшего целого числа.

Вариант 8

1. Составить схему алгоритма и программу для вычисления выражения

2. Посевная площадь картофеля в хозяйстве составляет S (га). Для его уборки используется N комбайнов производительностью Q 1 (га/час). Однако для уборки картофеля в запланированные D дней этого количества комбайнов недостаточно. Соседнее хозяйство предлагает в помощь комбайны производительностью Q 2 (га/час). Определить, сколько комбайнов соседей необходимо привлечь к уборке картофеля, если продолжительность рабочего дня составляет Т часов, а время для ежедневного технического обслуживания каждого комбайна – Е часов. В программе предусмотреть округление результата расчета до ближайшего большего целого числа.

Вариант 9

1. Составить схему алгоритма и программу для вычисления выражения:

.

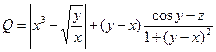2. Для уборки зерна используется R комбайнов производительностью F (га/ час) и L комбайнов производительностью W (га/час). Продолжительность рабочего дня комбайнов составляет К часов, время для ежедневного технического обслуживания каждого комбайна – Е часов. Определить, какую площадь уберут комбайны за М дней, если 1 комбайн производительностью F не работал два дня.

Вариант 10

1. Составить схему алгоритма и программу для вычисления выражения:

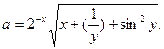
2. Фермер построил две теплицы одинаковой длины L (м). Первая теплица имеет в поперечном сечении форму прямоугольника со сторонами размером А на В (метров), вторая – полукруг радиуса R (м). Определить, сколько рулонов полиэтиленовой пленки необходимо фермеру для укрытия всей поверхности теплиц (включая торцы), если известно, что ширина одного рулона пленки составляет Н (м), а длина пленки в рулоне – D (м). В программе результат расчета округлить до ближайшего большего целого числа.

Вариант 11

1. Составить схему алгоритма и программу для вычисления выражения:

.

2. Садовый участок имеет форму равнобедренной трапеции, большее основание которой равно А (м), меньшее – В (м), высота – Н (м). Участок по всему периметру необходимо огородить забором. Определить, какое количество столбиков и сколько рулонов сетки необходимо заказать для забора, если расстояние между столбиками должно быть S (м), а длина одного рулона сетки – R (м).

Вариант 12

1. Составить схему алгоритма и программу для вычисления выражения:

.

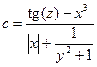2. Для уборки урожая используется К комбайнов производительностью А (га/час) и Р комбайнов производительностью В (га/час). Продолжительность рабочего дня комбайнов составляет Z часов, время для ежедневного технического обслуживания каждого комбайна – S часов. Определить, какую площадь уберут комбайны за К дней, если 1 комбайн производительностью А не работал два дня, а 1 комбайн производительностью В не работал три дня.

Вариант 13

1. Составить схему алгоритма и программу для вычисления выражения:

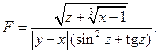
2. Длина, ширина и высота дома равна К (м), R (м) и N (м) соответственно. Дом имеет крышу, которая в поперечном сечении образует над потолком равносторонний треугольник. Поверхность в торце дома, заключенная между крышей и потолком, называется фронтоном. В доме имеется одна дверь размером А на В (метров) и 8 окон размером X на Y (метров). Стены дома планируется окрасить в зеленый цвет, фронтоны и двери – в желтый, а крышу – в коричневый. Окна решено не перекрашивать. Определить необходимое количество краски каждого цвета (в килограммах), если расход краски составляет Q (грамм на 1 м²).

Вариант 14

1. Составить схему алгоритма и программу для вычисления выражения:

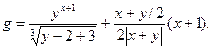
2.Хозяйство имеет А легковых и В грузовых автомобилей. Средний пробег за месяц эксплуатации одного легкового автомобиля составляет К (км), а грузового – М (км). Норма расхода бензина для легковых автомобилей составляет Z 1 (литров на 100 км), а дизтоплива для грузовых – Z 2 (литров на 100 км). Рассчитать годовую потребность автохозяйства в бензине и дизтопливе, общие затраты на топливо, если стоимость 1 литра бензина составляет С 1 (руб/ л), а дизтоплива – С 2 (руб/л).

Вариант 15

1. Составить схему алгоритма и программу для вычисления выражения:

.

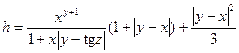2. Фермер имеет в своем хозяйстве N коров и М телят. Суточное потребление сена на одну корову составляет G (кг), на одного теленка – F (кг). На зиму фермер заготовил скирду сена длиной L (м) и поперечным сечением в форме равнобедренной трапеции с основаниями А и В (м) и высотой Н (м). Удельный вес сена составляет V (кг/м³). Рассчитать количество дней, в течение которых фермер сможет прокормить животных своим запасом сена. В программе предусмотреть округление результата до ближайшего меньшего целого числа.

Вариант 16

1. Составить схему алгоритма и программу для вычисления выражения:

2. В хозяйстве на уборке зерновых задействовано N комбайнов, имеющих производительность работы F (га/час) и М комбайнов с производительностью работы Q (га/час). Первому типу комбайнов предстоит убрать площадь S 1 (га), второму – S 2 (га). Часовой расход топлива при работе комбайнов составляет XI и Х 2 (л/час) соответственно. Определить, сколько тонн топлива потребуется для уборки урожая, если удельный вес топлива составляет Р (кг/л) и затраты хозяйства на топливо, если стоимость 1 тонны топлива составляет Z руб.

Вариант 17

1. Составить схему алгоритма и программу для вычисления выражения:

.

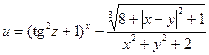2. В хозяйстве рожью засеяна площадь А (га), пшеницей – В (га). Урожайность ржи составляет С (ц/га), пшеницы D – (ц/га). Для доставки зерна с поля на элеватор используется N автомобилей грузоподъемностью P 1 тонн и M автомобилей грузоподъемностью Р 2 тонн. Продолжительность рабочего дня составляет Т часов, на выполнение одного рейса (с поля на элеватор и обратно) каждому автомобилю для доставки зерна с поля требуется R часов. Определить, сколько дней потребуется для доставки зерна с поля имеющимися автомобилями. Указание: при расчете числа рейсов, которые выполняют один автомобиль за день, в программе предусмотреть округление результата до ближайшего меньшего целого числа.

Вариант 18

1. Составить схему алгоритма и программу для вычисления выражения:

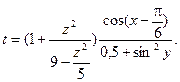
2. Тепличное хозяйство построило N новых теплиц длиной С (м). Поперечное сечение теплиц имеет форму полукруга радиусом R (м). Один торец теплицы имеет входную дверь размером А × В (метров). Необходимо укрыть всю поверхность теплиц (за исключением дверей) полиэтиленовой пленкой. Определить необходимое количество рулонов пленки, если ширина пленки в рулоне – Н (м), длина – D (м). В программе результат расчетов округлить до ближайшего большего целого числа.

Вариант 19

1. Составить схему алгоритма и программу для вычисления выражения:

.

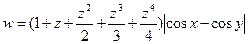2. На ручной уборке картофеля задействована группа из N студентов, причем ребята составляют С % от общего числа студентов, остальной состав группы -девушки. Скорость уборки картофеля ребятами за 1 час работы составляет Z м², а девушками – А (м²). Продолжительность рабочего дня студентов составляет M часов, из которых Т часов используется на обеденный перерыв. Определить, сколько гектаров поля уберут студенты за К дней.

Вариант 20

1. Составить схему алгоритма и программу для вычисления выражения:

.

2. Участок имеет форму квадрата с диагональю L м. Участок по всему периметру необходимо огородить забором. Определить, какое количество столбиков и сколько штакетин необходимо заказать для забора, если расстояние между столбиками должно быть С м, а на один метр забора дается М штакетин. В программе результаты округлить до ближайшего целого числа в большую сторону.

Вариант 21

1. Составить схему алгоритма и программу для вычисления выражения:

.

2. Автохозяйство имеет N автомобилей. Среднедневной пробег одного автомобиля составляет L км. Норма расхода бензина для автомобилей составляет Q (литров на 100 км). Определить, на сколько дней хватит бензина, если закуплено М тонн топлива (вес одного литра бензина – R кг). В программе результат расчета округлить до ближайшего меньшего целого числа.

Вариант 22

1. Составить схему алгоритма и программу для вычисления выражения:

.

2. В хозяйстве на уборке зерновых задействовано два комбайна, имеющие производительность работы F и X (га/час) соответственно. Первый комбайн убирает прямоугольное поле размером А × В (метров), площадь уборки для второго комбайна - в два раза больше. Часовой расход топлива при работе комбайнов составляет С и D (л/час) соответственно. Определить, сколько тонн топлива потребуется для уборки урожая, если удельный вес топлива составляет Q (кг/л), и затраты хозяйства на топливо, если стоимость 1 тонны топлива составляет W (руб.).

Вариант 23

1. Составить схему алгоритма и программу для вычисления выражения:

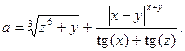
2. В хозяйстве рожью засеяна площадь X (га), пшеницей – на К % меньше. Урожайность ржи составляет Y (ц/га), пшеницы – на М % больше (ц/га). Для доставкизерна с поля на элеватор используются автомобили грузоподъемностью Р тонн. Продолжительность рабочего дня составляет Т часов, на выполнение одного рейса (с поля на элеватор и обратно) автомобилю требуется R часов. Определить, сколько автомобилей необходимо привлечь к работе, чтобы обеспечить доставку зерна с поля за N дней. Указание: при расчете числа рейсов, которые выполняет один автомобиль за день, в программе предусмотреть округление результата до ближайшего меньшего целого числа.

Вариант 24

1. Составить схему алгоритма и программу для вычисления выражения:

.

2. Для уборки картофеля используется N комбайнов производительностью Q 1 (г/час) и М комбайнов производительностью Q 2 (га/час). Продолжительность рабочего дня комбайнов составляет Т часов, время для ежедневного технического обслуживания каждого комбайна – Е часов. Определить, какую площадь уберут комбайны за К дней, если все комбайны производительностью Q 2 не работали два дня.

Вариант 25

1. Составить схему алгоритма и программу для вычисления выражения:

.

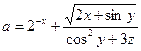2. В хозяйстве М теплиц длиной Z (м). Поперечное сечение теплиц имеет форму полукруга радиусом R (м). Для укрытия всей поверхности теплиц (включая торцы) хозяйство закупило F рулонов полиэтиленовой пленки шириной А (м). Длина пленки в одном рулоне – Q (м). Однако оказалось, что закупленной пленки недостаточно. Определить, сколько теплиц будет укрыто и сколько рулонов пленки необходимо купить дополнительно, чтобы укрыть оставшиеся. В программе результаты расчетов округлить до целых чисел.

Вариант 26

1. Составитьсхему алгоритма и программу для вычисления выражения:

.

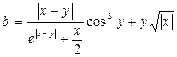2. Картофельное поле разбито на прямоугольные участки размером А × В (метров). На ручной уборке картофеля задействована группа из Z студентов, причем ребята составляют 68 % от общего числа студентов, остальной состав группы – девушки. Скорость уборки картофеля ребятами за 1 час работы составляет V (м²), а девушками – W (м²). Продолжительность рабочего дня студентов составляет Q часов, из которых Р часов используется на обеденный перерыв. Определить, сколько участков поля уберут студенты за К дней.

Вариант 27

1. Составить схему алгоритма и программу для вычисления выражения:

.

2. В хозяйстве К автомобилей. Среднедневной пробег одного автомобиля составляет W (км). Норма расхода бензина для автомобилей составляет А (литров на 100 км). Стоимость одного литра бензина – С (руб/л). Определить, на сколько дней хватит бензина, если на его покупку разрешено использовать денежную сумму в размере S рублей. В программе результат расчета округлить до ближайшего меньшего целого числа.

Вариант 28

1. Составить схему алгоритма и программу для вычисления выражения:

2. Фермер имеет в своем хозяйстве D коров и F телят. Суточное потребление сена на одну корову составляет К (кг), на одного теленка – Т (кг). Планируемый срок зимовки скота составляет Z дней. Сено на зиму фермер складывает в скирду, которая в поперечном сечении имеет форму полукруга диаметром Н (м). Удельный вес сена в скирде составляет Q (кг/м³). Рассчитать длину стога, необходимого фермеру, чтобы прокормить свое хозяйство зимой.

Вариант 29

1. Составить схему алгоритма и программу для вычисления выражения:

.

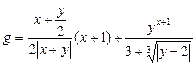2. В хозяйстве на уборке зерновых задействовано Z комбайнов, имеющих производительность работы Q (га/час), и М комбайнов с производительностью работы W (га/час). Первому типу комбайнов предстоит убрать площадь S (га), второму – на К % больше. Часовой расход топлива при работе комбайнов составляет D и G (л/час) соответственно. Определить, сколько тонн топлива потребуется для уборки урожая, если удельный вес топлива составляет Р (кг/л), и затраты хозяйства на топливо, если стоимость 1 тонны топлива составляет Т руб.

Вариант 30

1. Составить схему алгоритма и программу для вычисления выражения:

.

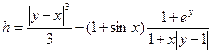2. Для уборки урожая используется К комбайнов производительностью А (га/час) и Р комбайнов производительностью В (га/час). Продолжительность рабочего дня комбайнов составляет Z часов, время для ежедневного технического обслуживания каждого комбайна – S часов. Определить, какую площадь уберут комбайны за К дней, если 1 комбайн производительностью А не работал два дня, а 1 комбайн производительностью В не работал три дня.

Вопросы для самоконтроля

1. Какие алгоритмы называют линейными?

2. Перечислите основные свойства алгоритма.

3. Какие алгоритмы называют разветвляющимися?

4. Что такое ветвь в блоке проверки условия?

5. Оператор условного перехода if, все варианты его использования.

Форма контроля – представить преподавателю отчет в письменном виде по изученному разделу.

Дата добавления: 2014-11-08