II уровень

Вариант 6

1. Вычислить C при любых заданных значениях x, a, b:

а ³ – b ² +2sin x, если x > а;

C = a ² + b ² – tg x, если x = а;

а – 2 b ⁴ + cos x, если x < а.

2. Определить количество неотрицательных чисел среди трех заданных a, b, c. Если таких чисел нет – вывести об этом сообщение.

3. Деревня А находится на расстоянии c км от железнодорожной станции и на расстоянии r км от другой деревни В (рисунок 8).

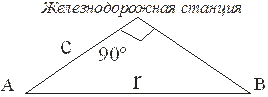
Рисунок 8

Определить, какая из деревень находится ближе к станции, напечатать сообщение об этом.

Вариант 7

1. Вычислить D при любых заданных значениях x, a:

(x – a)², если х > 0;

D = 2 x + a, если х = 0;

, если х < 0.

2. Определить, является ли число b наименьшим из четырех, не равных между собой a, b, c, d.

3. Даны две фигуры: квадрат со стороной a и прямоугольник со сторонами c, d. Определить, какая из фигур имеет больший периметр, и вывести сообщение об этом на печать.

Вариант 8

1. Вычислить C при любых заданных значениях x, a:

ах ² – 4, если x< –2;

x ⁴ – 1, если –2 £ x < 0;

C = х ³ + 8 х, если 0 £ x < 2;

4sin x, если x ≥ 2.

2. Определить, могут ли произвольные числа a, b, c служить длинами сторон треугольника.

3. Имеются 3 клубня шарообразной формы радиусами r1, r2, r3. Определить, сколько из них пройдет через круглое отверстие сепарирующего решета площадью s.

Вариант 9

1. Вычислить D для любых произвольных значений x, c:

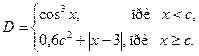
2. Составить алгоритм вычисления действительных корней квадратного уравнения ax² + bx + c = 0 по формулам:
x _1,2 = 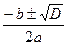, где D = b ² –4 ac.

3. Даны три действительных числа a, b, c. Вывести на печать те из них, которые принадлежать отрезку 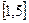, если таких чисел нет, то вывести на печать сообщение об этом.

Вариант 10

1. Вычислить C при любых заданных значениях x, a, b:

а ² – b ² +2sin x ², если x > а;

C = a ² + b – tg x, если x = а;

а – 2 b ⁴ + cos x, если x < а.

2. Даны три числа a, b, c. Определить, есть ли среди них отрицательные, вывести соответствующее сообщение на экран.

3. При осмотре леса лесник определил численность деревьев на контрольном участке: сосен – N1, елей – N2, берез – N3. Из них здоровыми являются соответственно M1, M2, M3, остальные повреждены. Определить, какого вида деревьев больше всего повреждено и вывести сообщение на печать.

Вариант 11

1. Вычислить F при любых заданных значениях x, c:

D =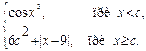

2. Вычислить Q = max (x, y, z) + x³. Значение x, y, z заданы.

3. Суточная норма кормления одной коровы составляет a кг сена, одной лошади – b кг сена. Определить, можно ли прокормить k коров и m лошадей в течение n дней, располагая массой p кг сена, если нет, то определить, сколько кг сена не хватает.

Вариант 12

1. Вычислить S при любых заданных значениях x, c:

S =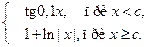

2. Среди 3-х точек с координатами (x ₁, y ₁), (x ₂, y ₂),(x ₃, y ₃) определить количество точек, лежащих в 3-ей четверти.

3. В колхозе имеется 3 комбайна ККУ-2А со средней производительностью s га в день и 5 комбайнов КПК-3 со средней производительностью p га в день. Будет ли выполнена колхозом уборка поля площадью s га в запланированный срок, составляющий 10 дней?

Вариант 13

1. Вычислить D при любых заданных значениях a, x:

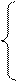| x | + a – 4, если а > 2;

D = 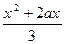, если а = 2;

4 х + a, если а < 2.

2. Даны две фигуры: квадрат со стороной a и круг с длиной окружности L. Определить, какая из фигур имеет большую площадь, и вывести эту площадь на печать.

3. Имеется 10 круглых луковиц диаметром d 1, 6 луковиц диаметром d2 и 15 луковиц диаметром d3. Радиус отверстия в сепарирующем решете p. Определить, сколько луковиц пройдет сквозь отверстие решета.

Вариант 14

1. Вычислить C при любых заданных значениях d, x:

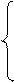сos x ² + d + 1, если d > 1;

C = 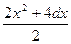, если d = 1;

8 х – d, если d < 1.

2. Заданы 4 неравных между собой числа a, b, c, d. Определить наибольшее из них и вывести на печать.

3. В квадрат со стороной x вписан круг. Определить, площадь какой фигуры больше: квадрата или круга и вывести сообщение на печать.

Вариант 15

1. Вычислить F при любых заданных значениях x, c:

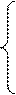| x | + x – 4, если x > 0.2

F = 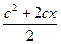, если x = 0.2

cos² x – 1, если x < 0.2

2. Среди 3-х точек с координатами (x ₁, y ₁), (x ₂, y ₂),(x ₃, y ₃) определить количество точек, лежащих в 4-ой четверти.

3. Каждая из трех доярок надоила за месяц (30 дней) соответственно Р1, Р2, Р3 литров молока. Определить, у какой доярки наибольший среднесуточный надой молока и вывести на экран ее номер.

Вариант 16

1. Вычислить T при любых заданных значениях a, d, b, c:

5, если d < a;

T = 4, если а ≤ d ≤ b;

3, если b < d < c;

2, если d ≥ c.

2. Определить количество положительных чисел среди четырех a, b, c, d.

3. Определить, можно ли огородить изгородью длиной r земельный участок, имеющий форму равнобедренной трапеции с основаниями c, d и высотой h.

Вариант 17

1. Вычислить D при любых заданных значениях x, a, z:

| ax – 3|, если х < 2;

D = 8 x – 1, если 2 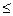х < 3;

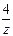+ a ³, если x 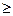3.

2. Определить, какая из сторон k, l, m прямоугольного треугольника является его гипотенузой, и вывести ее значение на печать.

3. Определить, какая из трех точек с координатами А(x ₁, y ₁), В(x ₂, y ₂), С(x ₃, y ₃) наиболее удалена от начала координат и вывести на печать ее номер.

Вариант 18

1. Вычислить Z при любых заданных значениях a, b, x, c:

a x ²/2 + b x – c, если x 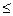1;

Z = x + 1,5, если 1 < х < 2;

2 x ² – b, если x ³ 2.

2. Проверить, является ли треугольник со сторонами a, b, c равнобедренным и вывести на экран соответствующее сообщение.

3. Даны две фигуры: квадрат с диагональю d ипрямоугольная трапеция со сторонами x, y, z (рисунок 9). Определить, какая из фигур имеет больший периметр, сообщение вывести на печать.

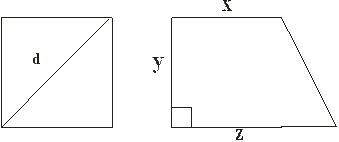
Рисунок 9 – Квадрат с диагональю d ипрямоугольная трапеция со сторонами x, y, z

Вариант 19

1. Вычислить T для любых произвольных значений х и с:

T =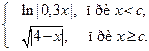

2. В прямоугольном треугольнике заданы три стороны k, l, m. Вывести на печать значение гипотенузы и найти площадь треугольника.

3. Заданы четыре переменные x, y, z, d. Найти и вывести на печать количество переменных, попавших в интервал от –5 до 5, если таких нет – дать сообщение.

Вариант 20

1. Вычислить D при любых заданных значениях x, a, b:

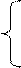ax + b, при х £ 0;

D = |b| – 2, при 0 < x £ 1;

| а | – х ², при х >1.

2. Вычислить Q = min (a, b, c) + z. Значения a, b, c, z заданы.

3. Даны две фигуры: квадрат с диагональю d ипрямоугольная трапеция со сторонами x, y, z. Определить, какая фигура имеет большую площадь, сообщение вывести на печать (см. рисунок 9).

Вариант 21

1. Вычислить Y при любых заданных значениях a, x, b:

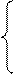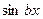, при x < a;

Y = сos ax, при а £ x £ b;

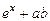, при x > b.

2. Среди 3-х точек с координатами (x₁, y ₁), (x ₂, y ₂),(x ₃, y ₃) определить количество точек, лежащих в 1-ой четверти.

3. Имеются четыре результата t1, t2, t3, t4 (сек.) в беге на 100 метров. Вывести на печать результат и номер победителя.

Вариант 22

1. Вычислить Z при любых заданных значениях a:

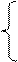asinx², если a ≤ –3;

Z = 1, если –3 < a < 4;

сos(a + 1), если a ≥ 4.

2. Среди 3-х точек с координатами (x ₁, y ₁), (x ₂, y ₂),(x ₃. y ₃) определить количество точек, лежащих в 2-ой четверти и вывести на экран их координаты.

3. Четыре студента сдали экзамен по физике и получили соответственно оценки x, y, z, d. Определить и вывести на печать номера студентов, оценка которых превышает средний балл по предмету.

Вариант 23

1. Вычислить S при любых заданных значениях a, b, c:

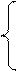
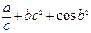, при c < 3;

S = cos³ a – c, при 3 £ c £ 7;

ac + bc ³ + 2, при c > 7.

2. Даны две фигуры: квадрат с периметром z и круг с длиной окружности c. Определить, какая из фигур имеет большую площадь, и вывести эту площадь на печать.

3. Четыре студента сдали экзамен по физике и получили соответственно оценки a, b, c, d. Определить и вывести на печать количество и номера студентов, которые получили по экзамену оценку 9.

Вариант 24

1. Вычислить Z при любых заданных значениях x:

x ³ – 3 x + 8, при х £ 0;

Z = 4, при 0 < x £ 1;

1 / (x ³ – 3 x + 8), при х >1.

2. Среди трех чисел a, b, c есть пара равных. Заменить их нулями и все числа вывести на печать.

3. Имеются четыре результата z1, z2, z3, z4 ( м ) по прыжкам в высоту. Вывести на печать количество и номера спортсменом, которые прыгнули выше заданного норматива L (м).

Дата добавления: 2014-11-08