Численными методами

Лекция 2 Решение нелинейных уравнений

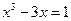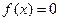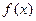При решении любое нелинейное уравнение, например , предварительно приводится к виду , т. е. , при этом функции могут быть алгебраическими, у которых над аргументом х выполняются лишь арифметические операции, и трансцендентными, которые содержат, кроме того, показательные, логарифмические, тригонометрические функции аргумента х. Такие уравнения далеко не всегда можно решить точно, а для практических расчетов точное решение не всегда является обязательным. Поэтому важное значение с развитием вычислительной техники приобрели способы приближенного вычисления корней и оценки их точности.

Данная процедура состоит из двух этапов: 1) отделение корней, т. е. выделение таких отрезков [ a, b ], в каждом из которых находится только один корень уравнения или нахождение первоначальных приближений корней; 2) уточнение корней, т. е. нахождение их на найденных отрезках с заданной степенью точности.

Простейшим способом отделения корней является графический. На графике функции 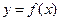определяются отрезки [ a, b ], в пределах которых лежат точки пересечения функции с осью 0 Х, являющимися приближенными значениями корней. Например, при решении уравнения сначала вычисляем значения функции 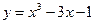, по заданным значениям аргумента х (таблица 1) и затем по полученным данным строим график (рисунок 4).

Таблица 1 – Результаты табулирования функции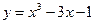

х	–3	–2	–1
y	–19	–3		–1	–3

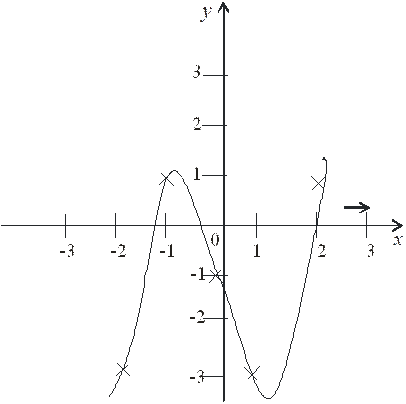
Рисунок 4 – График функции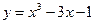

Как видно из графика, уравнение имеет 3 корня на отрезках [–2, –1], [–1, 0] и [1, 2].

Отделить корни можно также программным способом. Для составления алгоритма решения данной задачи рассмотрим поведение функции 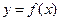на интервале от х _нач до х _кон с шагом h (рисунок 5).

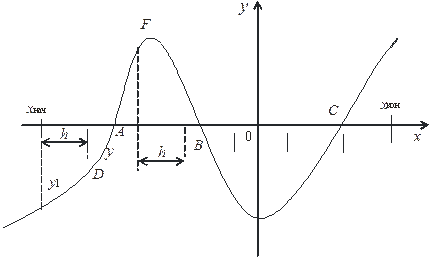
Рисунок 5 – График функции 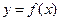при наличии корней

Как видно из рисунка, корни уравнения находятся в точках А, В и С, где 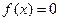. Данные точки можно обнаружить, рассчитывая значения функции 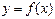от х _нач до х _кон с шагом h и наблюдая за изменением ее знака. Так, в точке А значение функции изменяется с «-» на «+», а в точке В с «+» на «-» и т. д. Обнаружить изменение знака функции можно путем перемножения двух ее значений, вычисленных от аргументов х, находящихся в соседних точках на расстоянии h одно от другого. Для точки А, например, это будут значения функции D и F.

Отделение корней по программному методу реализует алгоритм, представленный на рисунке 6.

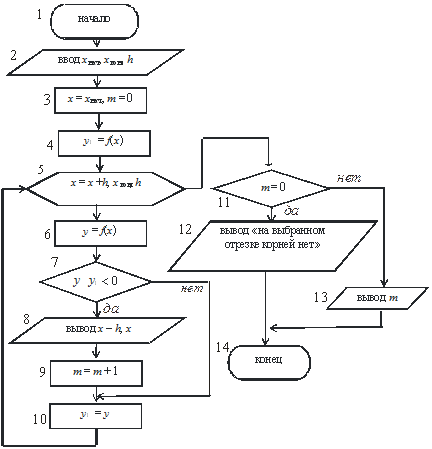
Рисунок 6 – Схема алгоритма отделения корней функции f(x) на отрезке [ х _нач, х _кон]

В блоке 2 вводятся начальное значение аргумента функции х _нач, конечное х _кон и шаг его изменения h.

В блоке 3 принимается текущее значение х за х _нач и количество корней m = 0, а в блоке 4 вычисляется первоначальное значение функции у ₁ при х = х _нач.

Блок 5 организует цикл по изменению х от х + h до х _кон с шагом h. В блоке 6 вычисляется очередное значение функции в точке 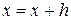(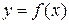). Затем в блоке 7 проверяется, не пересекла ли функция 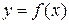ось ОХ. В случае отсутствия пересечения 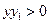полученное значение у в блоке 10 запоминается как у ₁, а в блоке 5 значение х опять изменяется на величину шага h. Затем в блоке 6 снова вычисляется у и в блоке 7 проверяется функция на изменение знака. Так как в этом случае (точки D и F на рисунке 5), то в блоке 8 выводятся значения аргумента х - h и x, в пределах которых находится корень уравнения, а в блоке 9 фиксируется увеличение количества найденных корней на единицу.

Циклический процесс повторяется до принятого конечного значения аргумента х _кон. В результате будут найдены отрезки, на которых находятся корни нелинейного уравнения (около точек А, В, С на рисунке 5.).

Вопросы для самоконтроля

1. В чем сущность численных методов вычисления определенного интеграла?

2. От чего зависит точность вычисления интеграла?

3. В чем отличие метода трапеций от метода прямоугольников?

4. Чем объясняется более высокая точность при вычислении интеграла методом трапеций?

5. Из каких этапов состоит процесс решения нелинейных уравнений?

6. Чем характерна область, где находится корень уравнения?

7. Как в алгоритме и программе определяется область нахождения корня?

8. В чем сущность нахождения корня с необходимой точностью в заданной области?

Дата добавления: 2014-11-08