Коефіцієнт кореляції

Коефіцієнти різних рівнянь регресії при неоднакових одиницях вимірювання результуючої або факторної змінної не можна порівнювати. На практиці часто виникає необхідність порівняння двох чи декількох рівнянь регресії та оцінювання міцності їхнього зв’язку. Таке порівняння різних рівнянь регресії можливе на основі певних безрозмірних одиниць вимірювання.

Для лінійної форми зв’язку між результуючою і факторною змінними найчастіше використовують коефіцієнт кореляції r - безрозмірний показник, що характеризує міцність і напрям лінійної залежності між змінними X i Y.

Коефіцієнт кореляції обчислюють т. ч.:

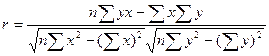
Функція КОРРЕЛ(масив1;масив2) обчислює оцінку коефіцієнта кореляції випадкових величин X i Y.

Коефіцієнт кореляції – використовується для оцінки ступеня лінійної залежності між двома змінними X та Y. Може приймати значення від -1 до +1. При додатних значеннях коефіцієнта кореляції із зростанням факторної змінної x збільшується середнє значення результуючої змінної y; при від’ємних – із зростанням факторної змінної x середнє значення результуючої змінної зменшується y.

Знак коефіцієнта кореляції збігається із знаком коефіцієнта регресії .

Якщо значення коефіцієнта кореляції дорівнює за модулем одиниці, то це означає, що між результуючою і факторною змінними існує функціональний зв'язок. Чим ближче до одиниці, тим сильніший лінійний зв’язок між змінними x і y.

Якщо коефіцієнт кореляції близький до нуля (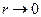), то зв'язок між змінними x та y відсутній (говорять, що випадкові величини x та y некорельовані, але це не означає, що вони незалежні).

В економічних дослідженнях при значеннях коефіцієнта кореляції 0,7-0,9 зв'язок вважають міцним (сильним), 0,9-0,99 – дуже міцним.

Якщо , то немає змісту шукати пряму, яка найкращим чином описує експериментальні дані.

Така оцінка є експертною і наближеною. Для точнішої оцінки міцності зв’язку необхідно ще враховувати зміст і мету дослідження, обсяг початкових спостережень тощо.

Приклади, як можуть виглядати різні кореляції щодо міцності і напрямку взаємозв’язку.

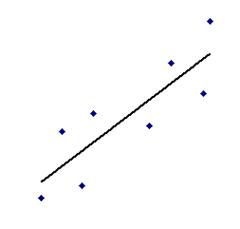r= +0,85	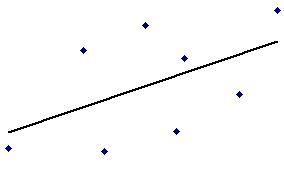r= -0,52
r= +1	r= -1

Діаграми розсіювання з різними кореляціями

Властивості коефіцієнта кореляції:

Кореляція не має одиниць вимірювання. Це означає, що якщо поміняти одиниці вимірювання x та y, то кореляція не зміниться.

Значення x та y в наборі даних можна поміняти місцями, кореляція при цьому не зміниться.

Для нашого прикладу:

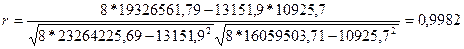
Значення коефіцієнта кореляції 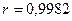свідчить про те, що зв'язок між доходом і чистим прибутком фірми є досить міцним.

Оскільки коефіцієнт кореляції високий (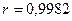), то пряма лінія найкращим чином підходить експериментальним даним.

Оскільки між x та y спостерігається кореляція, то між ними існує лінійна залежність. Це означає, що таку залежність можна представити у вигляді прямої лінії. Якщо нам відомі b₀, b₁ то ми можемо підставити значення x і спрогнозувати середнє значення y.

Кореляція вимірює строгість лінійної залежності між числовими змінними.

Якщо між двома змінними існує кореляція, то це не обов’язково означає, що між ними є ще і причинно-наслідковий взаємозв’язок.

Оцінку якості побудованої моделі дає коефіцієнт детермінації R².

Коефіцієнт детермінації дає відповідь на питання, чи справді зміна значення у лінійно залежить саме від зміни значення х, а не відбувається під впливом інших випадкових факторів.

Значення коефіцієнта детермінації набуває значень від 0 до 1 (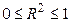.) і характеризує, якою мірою варіація (зміна) залежної змінної y визначається варіацією незалежної змінної x. Чим ближчий він до 1, тим більше варіація залежної змінної визначається варіацією незалежної змінної.

Як правило вважається, якщо , то побудована модель є адекватною реальній дійсності.

Якщо , то залежність між у та x є недостатньою для прийняття моделі. Тоді модель не можна використовувати для економічного аналізу і знаходити значення прогнозу

Для нашого прикладу R² =0,9964. Отже, впливом доходу пояснюється близько 99,64 % варіації прибутку.

Висновок про адекватність лінійного рівняння регресії експериментальним даним робимо на основі критерію Стьюдента.

Обчислимо t -статистику: =40,622

Якщо 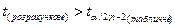, то коефіцієнт кореляції генеральної сукупності відмінний від нуля, а кореляційний зв'язок є значним з надійністю 0,95.

Якщо 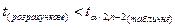, то модель підібрана невдало, так як вона не узгоджується з експериментальними даними

Отже, вплив доходу на прибуток є значним.

За критерієм Стьюдента і надійністю Р=0,95 модель можна вважати адекватною експериментальним даним (якісною). Коефіцієнт детермінації статистично значимий і включені у регресію фактори достатньо пояснюють стохастичну залежність показника.

Зауваження. Дана формула застосовується, для вибірки, коли n<50.

Якщо n>100, використовується формула: 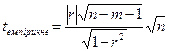. Величина t має розподіл близький до розподілу Стьюдента (t -розподілу).

Висновки.

Економетрична модель 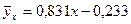кількісно описує зв'язок чистого прибутку і доходу фірми.

Коефіцієнт b₀= -0,233 економічного змісту не має.

Коефіцієнт регресії b₁= 0,831 показує, що при збільшенні доходу фірми на 1 тис. грн. середнє значення чистого прибутку фірми буде збільшуватися на 0,831 тис. грн., тобто на 831 грн.

Коефіцієнт еластичності чистого прибутку залежно від доходу фірми:

EY / X=b₁: 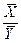=0,831: 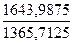=0,7

Отже, із збільшенням доходу фірми на 1 % чистий прибуток зростає на 0,7 %.

Коефіцієнт кореляції R =0,9982 свідчить про досить тісний зв’язок між прибутком та основними фондами.

Значення коефіцієнта детермінації R² =0,9964 показує, що зміна (коливання) значення чистого прибутку фірми на 99,64 % залежить від зміни (коливання) значення доходу і на 0,36 % залежить від зміни значень інших факторів, які в цій регресійній моделі не розглядалися.

З надійністю P =0,95 можна вважати, що отримана модель 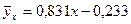адекватна до експериментальних даних і на підставі прийнятої моделі проводити економічний аналіз і знаходити значення прогнозу.

Оптимальна пряма для прогнозування прибутку від доходу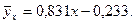

Завдання Спрогнозувати прибуток, якщо дохід x=2000.

Ми можемо припустити, що очікуваний (прогнозований) прибуток при доході x=2000 за даною моделлю становить

Дата добавления: 2014-11-16