Черт. 25. К примеру расчета 13

ПРИМЕРЫ РАСЧЕТА

Расчет наклонных сечений

на действие поперечной силы

Пример 13. Дано: железобетонная плита пере­крытия с размерами поперечного сечения по черт. 25; бетон тяжелый класса В15 (R_b = 7,7 МПа и R_bt = 0,67 МПа при g _{b 2} = 0,9; E_b = 20,5 · 10³ МПа); ребро плиты армировано плоским сварным кар­касом с поперечными стержнями из арматуры класса А-III, диаметром 8 мм (A_sw = 50,3 мм²; R_sw = 285 МПа; E_s = 2 · 10⁵ МПа), шагом s = 100 мм; временная эквивалентная нагрузка v = 18 кН/м; нагрузка от собственного веса плиты и пола g = 3,9 кН/м; поперечная сила на опоре Q_max = 62 кН.

Требуется проверить прочность наклонной поло­сы ребра между наклонными трещинами, а также прочность наклонных сечений по поперечной силе.

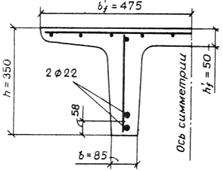
Расчет. h ₀ = 350 – 58 = 292 мм. Прочность наклонной полосы проверим из условия (47).

Определим коэффициенты j_{w 1} и j_{b 1}:

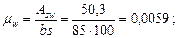
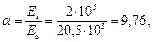
отсюда j_{w 1} = 1 + 5a m_w = 1 + 5 · 9,76 · 0,0059 = 1,29 < 1,3;

для тяжелого бетона b = 0,01;

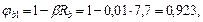
тогда

т. е. прочность наклонной полосы обеспечена.

Прочность наклонного сечения по поперечной силе проверим из условия (50).

Определим величины M_b и q_sw:

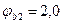(см. табл. 21);

так как 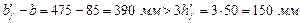, принимаем 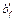– b = 150 мм, тогда:

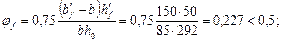
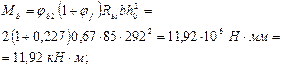
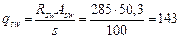Н/мм (кН/м).

Определим значение Q_b,min, принимая j_{b 3} = 0,6:

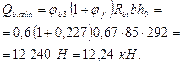
Поскольку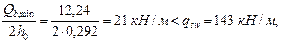

условие (57) выполняется, и, следовательно, значе­ние М_b не корректируем.

Согласно п. 3.32 определим длину проекции невыгоднейшего наклонного сечения с:

кН/м (Н/мм),

поскольку 0,56 q_sw = 0,56 · 143 == 80 кН/м > q ₁ = 12,9 кН/м, значение с определим только по формуле

м.

Тогда

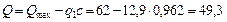кН.

Длина проекции наклонной трещины равна:

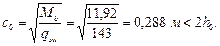
Поскольку c ₀ = 0,288 < h ₀ = 0,292 м, принимаем c ₀ = h ₀ = 0,292 м, тогда Q_sw = q_swc ₀ = 143 · 0,292 = 41,8 кН.

Проверим условие (50):

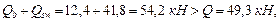
т. е. прочность наклонного сечения по поперечной силе обеспечена. Кроме того, должно выполняться требование п. 3.29:

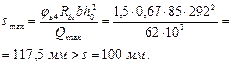
Условия п. 5.69 s < h /2 = 350/2 = 175 мм и s < 150 мм также выполняются.

Пример 14. Дано: свободно опертая железобетон­ная балка перекрытия пролетом l = 5,5 м; времен­ная равномерно распределенная эквивалентная нагрузка на балку v = 36 кН/м; постоянная нагрузка g = 14 кН/м; размеры поперечного сечения b = 200 мм, h = 400 мм, h ₀ = 370 мм; бетон тяжелый класса В15 (R_b = 7,7 МПа; R_bt = 0,67 МПа при g _{b 2}= 0,9); хомуты из арматуры класса А-I (R_sw = 175 МПа).

Требуется определить диаметр и шаг хомутов у опоры, а также выяснить, на каком расстоянии от опоры и как может быть увеличен шаг хомутов.

Расчет. Наибольшая поперечная сила в опор­ном сечении равна:

кН,

где q = v + g = 36 +14 = 50 кН/м.

Определим требуемую интенсивность хомутов приопорного участка согласно п. 3.33б.

Из формулы (52) при j_f = 0 и j_{b 2} = 2,0(см. табл. 21) получим

Согласно п. 3.32,

кН/м (Н/мм);

кН.

Так как

интенсивность хомутов определим по формуле (63):

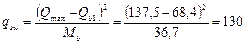кН/м (Н/мм).

При этом, поскольку

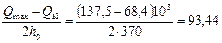Н/мм < 130 Н/мм,

оставляем q_sw = 130 Н/мм.

Согласно п. 5.69, шаг s ₁ ó опоры должен быть не более h /2 = 200 и 150 мм, а в пролете = 300 и 500 мм. Максимально допустимый шаг у опоры, согласно п. 3.29, равен:

мм.

Принимаем шаг хомутов у опоры s ₁ = 150 мм, а в пролете — 2 s ₁ = 300 мм, отсюда

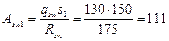мм².

Принимаем в поперечном сечении два хомута диаметром по 10 мм (А_sw= 157 мм²).

Таким образом, принятая интенсивность хомутов у опоры и в пролете балки будет соответственно равна:

Н/мм;

Н/мм.

Проверим условие (57), вычислив Q_b,min:

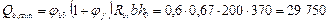H.

Тогда

Следовательно, значения q_{sw 1} и q_{sw 2} не коррек­тируем.

Определим, согласно п. 3.34, длину участка l ₁ с интенсивностью хомутов q_{sw 1}. Так как q_{sw 1} — q_{sw 2}= q_{sw 2} = 91,6 H/мм > q ₁ = 32 Н/мм, значение l ₁ вычислим по формуле

(здесь 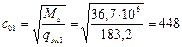мм).

Принимаем длину участка с шагом хомутов s ₁ = 150мм равной 1,64 м.

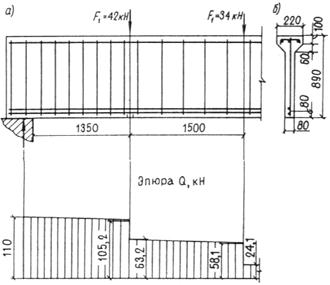
Пример 15. Дано: железобетонная балка покры­тия, нагруженная сосредоточенными силами, как показано на черт. 26, а; размеры поперечного сечения — по черт. 26, б, бетон тяжелый класса В15 (R_bt = 0,67 МПа при g _{b 2} = 0,9); хомуты из армату­ры класса А-I (R_sw = 175 МПа).

Требуется определить диаметр и шаг хомутов, а также выяснить, на каком расстоянии и как может быть увеличен шаг хомутов.

Расчет. Сначала определим, согласно п. 3.31, величину M_b:

(см. табл. 21);

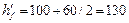мм (см. черт. 26, б);

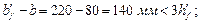
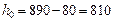мм;

Дата добавления: 2014-11-16